Решение уравнений методом Крамера.
Картинка 1.
Картинка 2.
Картинка 3
Работа в SciLab. Формирование матриц и векторов, составляя их из заранее заданных Пример:
4.2. Знак «:» Указывая знак «:» вместо индекса при обращении к массиву, можно иметь доступ к группам его элементов.
Пример.
Нахождение собственных чисел и собственных векторов квадратной матрицы, функция spec(M)
Пример.
Задание 1. Найти собственные значения и собственные вектора линейных преобразований, заданных в некотором базисе матрицами. 1.1.
Решение систем линейных уравнений методом приведения к треугольному виду.
Пример.
Задание 2. Решить систему уравнений методом исключения неизвестного. 2.1. Ответ 2.1: x = (1. - 3. 2. - 2.) Ответ 2.2. x = (2. 1. - 3. 1)
Связь между матрицами одного и того же преобразования в разных базисах.
Связь между матрицами одного и того же преобразования в разных базисах выражается формулой
Пример 1. Линейное преобразование Решение. Обозначим через Из условия задачи ясно, что матрица перехода от базиса
Задание 3: 3.1. Линейное преобразование Найти его матрицу в базисе:
3.2. Найти матрицу в базисе
Решение уравнений методом Крамера.
Задание 4. Решить системы уравнений методом Крамера.
4.1.
|
.
. 1.2. 
2.2. 
, где
– матрица линейного преобразования 
в базисе 
,
– матрица линейного преобразования 
в базисе 
, а 
– матрица перехода от базиса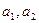 
имеет матрицу 
. Найти его матрицу в базисе 
.
. Тогда имеем 
. Найдем 
, тогда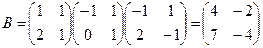 
.
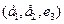имеет матрицу 
.
, где 
