Некоторые теории категории числа.

Оригинальную теорию числа разработали Дамурет и Пишон. Они выделяют во французском языке категорию «количественности» (quantitude), различая в ней два аспекта: считаемость (PIItation) и целостность (blocalité). По считаемости имена делятся на несчитаемые (massiers) и считаемые (nombriers). Эта категория выражается артиклями: du mouton (несчитаемость), un/des moutons (считаемость). Категория целостности выражается флексией и показывает, мыслится ли объект как непрерывное целое (blocalité continue: du, un mouton) или как прерывистое соединение объектов (blocalité discontinue: des moutons). Сочетание этих двух категорий изображается ими так:

Авторы приходят к выводу, что различие между считаемостью и несчитаемостью во французском языке образует грамматическую категорию благодаря тому, что оно выражается артиклем. По их мнению, любое считаемое существительное может благодаря артиклю перейти в разряд несчитаемых (un bœuf →;du boeuf) и наоборот (du verre →; un verre). Вместе с тем они отмечают и возможность разнообразных семантических сдвигов, причем не всегда можно предусмотреть характер этого сдвига: если du bœuf означает «мясо быка», то du cygne – «перья лебедя», de l'hermine – «мех горностая» и т.п.

Исходя из теории Дамурета и Пишона (см. среднюю колонку таблицы), в теоретической грамматике высказывалось мнение, что в категории числа имеется три субкатегории: единственное число, множественное число и несчисляемость (недискретность), выражаемые артиклями: le/un, les/des и du, причем в значении определенности нет особого средства для выражения недискретности [26 (1), с. 31–32]. Последнее не совсем точно, ибо определенность недискретных объектов выражается артиклем le, противопоставленным du: le/du pain. Следовательно, во французском языке имеются два функциональных варианта артикля le: вариант le₁ выражающий определенность дискретных объектов (le/un livre), и вариант le₂ выражающий определенность недискретных веществ (le/du pain). Соотношение трех значений (дискретность, определенность, число) в этой теории может быть представлено так:

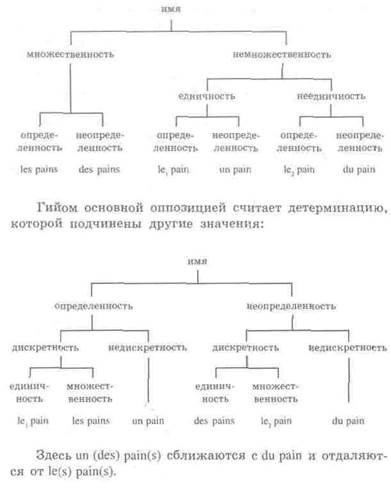
Таким образом, оппозиция дискретность/недискретность и единичность/множественность выстраивается в один ряд.

В. Е. Щетинкин [61], видя главное средство выражения числа в артиклях, считает основным противопоставлением множественность/ немножественность, причем в последнем значении выделяется вторичная оппозиция: единичность–неединичность (несчисляемость).

Недискретность (неединичность + немножественность) здесь интеPIIретируется как субкатегория противопоставления множественность/немножественность (эта точка зрения отражает аспект blocalité Дамурета-Пишона). Здесь un pain сближается с du pain и отделяется от des pains. Это соотношение может быть выражено схемой: