Нестационарная теплопроводность тел
1.1. Условие задачи Исследовать процесс нагрева железобетонной плиты при ее термической обработке, имеющей размеры s × b × l. Определить распределение температуры по толщине плиты и расход теплоты на единицу ее объема по истечении времени τ в зависимости от интенсивности теплообмена между греющей средой и поверхностью плиты. В начале термической обработки температура по всему объему плиты была одинаковой и равной tп. Температура греющей среды в процессе нагрева плиты поддерживалась постоянной и равной t0. Обогрев плиты симметричный. Время процесса нагрева τ определить из условия, что температура на поверхности плиты оказалась равной tс. Скорость потока водяного пара относительно поверхности плиты w. Данные к заданию приведены в табл. 1. Таблица 1.1 - Исходные данные
1.2 Решение задачи
Рисунок 1.1 – Схематическое изображение нагрева плиты На первом этапе нужно определить критерий Био Bi. Для этого найдем критерии Рейнольдса Re, Нуссельта Nu для пара и коэффициент теплоотдачи от потока пара к поверхности плиты α;:
где w – скорость потока пара, м/с; l – высота плоской стенки, м;
где Prж и Prс – числа Прандтля для потока пара и поверхности стенки соответственно;
Коэффициент теплоотдачи
где
Таблица 1.2 - Полученные значения Re, Nu, α
Определим критерий Био, представляющий собой отношение термического сопротивления теплопроводности материала плиты к термическому сопротивлению теплоотдачи от потока пара к плите:
где S – толщина плиты, м.
Таблица 1.3 – Полученные значения Bi
Исходя из критерия Био, находим значения δi из трансцендентального уравнения (1.5).
Таблица 1.4 - Полученные значенияδi
Температура на поверхности плиты находится из уравнения (1.6):
где
Тогда при помощи итерационного метода на ЭВМ вычисляется значение критерия Фурье, используя формулу (1.6). Таблица 1.5- Полученные значения Fo
Критерий Фурье, характеризующий изменение температуры во времени, можно также найти по формуле (1.7):
где Используя формулу (1.7), можно выразить и вычислить время нагрева плиты до заданной температуры tc:
Таблица 1.6 - Полученные значения τ.
Количество тепла, подведенное через единицу площади поверхности при ее нагреве от начальной температуры до температуры, равной температуре потока пара, определится по формуле:
Количество тепла Q (Дж/м2), подведенное к единице площади поверхности плиты за время τ можно рассчитать следующим образом:
Таблица 1.7 – Полученные значения Q(τ)
Для того, чтобы построить график распределения температуры по толщине сечения плиты найдем значения температуры в точках хi=(0; 0,25·s/2; 0,5·s/2; 0,75·s/2; 1·s/2) no формуле:
Таблица 1.8 – Полученные значения tx
График τ=f(w) изображены на рисунках 1.2, 1.3, Q=f(τ) изображены на рисунках 1.4, 1.5, α=f(w) изображены на рисунках 1.6, 1.7, t=f(x) изображены на рисунках 1.8 и 1.9.
Рисунок 1.2. График зависимости скорости потока пара (W) от времени нагрева (τ) при первой температуре пара (tп1=110°С)
Рисунок 1.3. График зависимости скорости потока пара (W) от времени нагрева (τ) при второй температуре пара (tп2=150°С)

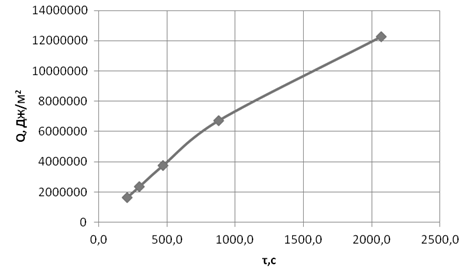
Рисунок 1.4. График зависимости кол-ва тепла подведенного к единице площади поверхности (Q) за время τ при первой температуре пара (tп1=110°С)
Рисунок 1.5. График зависимости кол-ва тепла подведенного к единице площади поверхности (Q) за время τ при второй температуре пара (tп2=150°С)
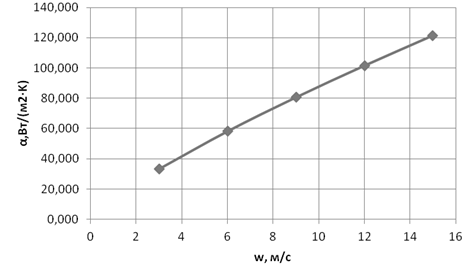
Рисунок 1.6. График зависимости коэффициента теплоотдачи от скорости потока пара (w) при первой температуре пара (tп1=110°С)
Рисунок 1.7. График зависимости коэффициента теплоотдачи от скорости потока пара (w) при второй температуре пара (tп2=150°С)
Рисунок 1.8. График зависимости распределения температуры по толщине плиты при разных скоростях при первой температуре пара (tп1=110°С)
Рисунок 1.9. График зависимости распределения температуры по толщине плиты при разных скоростях при второй температуре пара (tп2=150°С) Вывод Из графика зависимости распределения коэффициента теплоотдачи от скорости движения пара видно, что с увеличением скорости коэффициента теплоотдачи увеличивается. Из графика зависимости распределения времени нагрева поверхности плиты до заданной температуры от скорости движения пара видно, что с увеличением скорости время нагрева уменьшается. Из графика зависимости распределения количества теплоты, от времени нагрева поверхности плиты до заданной температуры видно, что с увеличением времени нагрева количества теплоты увеличивается. Так как время нагрева поверхности плиты зависит от температуры и скорости потока пара, то количество теплоты, переданное на нагрев поверхности плиты, также будет зависеть от этих параметров. Из графика можно сделать вывод, что при увеличении температуры и скорости потока пара время на нагрев поверхности плиты будет уменьшаться, и соответственно количество теплоты также будет убывать. Из графика зависимости распределения температуры по толщине плиты следует, что с увеличением температуры и скорости потока пара, температура внутри плиты, за время нагрева поверхности плиты до заданной температуры, практически остается неизменной. В этой работе мы показали, что изменение температуры по сечению плиты зависит от критерия Био. Также мы определили расход теплоты на нагрев поверхности плиты до заданной температуры. 2. Передача теплоты через оребренную поверхность плоской стенки 2.1 Условие задачи Исследовать эффективность оребрения поверхности плоской стенки в зависимости от высоты ребра h и теплопроводных свойств его материала при граничных условиях третьего ряда. Плоская стенка с размерами по высоте 800 мм и ширине 1000 мм оребрена продольными ребрами прямоугольного сечения. По ширине стенки размещено 50 ребер.
Рисунок 2.1 – Схема ребра Для оптимального размера ребра выполнить расчёты распределения температуры, определить плотность теплового потока, передаваемого ребром, оценить вклад отвода теплоты к окружающему воздуху оребренной поверхностью стенки по сравнению с неоребренной. Данные к заданию приведены в таблице 2.1.
Таблица 2.1 - Исходные данные
2.2 Решение задачи Рассмотрим случай для плоской стальной стенки с высотой ребра h=0,01 при свободной конвекции (т.е. скорость внешнего потока воздуха w=0 м/с). Определим критерий Грасгофа по формуле:
Найдем произведение критерия Грасгофа на критерий Прандтля для выбора расчетной формулы нахождения критерия Нуссельта:
следовательно:
Определим коэффициент теплоотдачи α; от ребра к окружающему воздуху по формуле:
Определим параметр ребра m по формуле:
Рассчитаем тепловой поток, передаваемый через основание ребра по формуле:
Максимальный тепловой поток, передаваемый ребром, при абсолютной теплопроводности материала ребра (λ=∞) и при температуре по всей поверхности ребра, равной температуре в его основании, определяется по выражению:
Тогда отношение действительного теплового потока к максимальному оценивает коэффициент эффективности продольного ребра прямоугольного сечения:
Для того, чтобы построить график распределения температуры по высоте ребра найдем значения температуры в точках хi=(0; 0,25∙h; 0,5∙h; 0,75∙h; h) по формуле:
Таким образом, получили следующее распределение:
Оценим вклад отвода теплоты к окружающему воздуху оребренной поверхностью по сравнению с неоребренной (ε;). Для этого найдем тепловой поток, передаваемый через всю оребренную поверхность Qоребр и поток через неоребренную поверхность плоской стенки Qнеор:
где Q – тепловой поток, передаваемый через основание ребра, (Вт); α; – коэффициент теплоотдачи от ребра к окружающему воздуху, (Вт/м2∙К).
где
Если
тогда Следовательно,
Следовательно, вклад отвода теплоты равен:
Дальше аналогично рассчитываем все необходимые параметры для определения распределения температуры, потока теплоты, поверхностной плотности теплового потока, коэффициента эффективности продольного ребра прямоугольного сечения в условиях свободной конвекции, для оставшихся четырех высот (h) для стали, пяти высот (h) для латуни и меди. Проводим оценку вклада отвода теплоты к окружающему воздуху оребренной поверхностью стенки по сравнению с неоребренной. Результаты расчета для меди и стали приведены в таблице 2.2. Таблица 2.2 – Результаты расчета передачи теплоты при свободной конвекции
Рассмотрим случай для плоской стальной стенки с высотой ребра h=0,01 при вынужденной конвекции, скорость внешнего потока воздуха w=2 м/с. Определим критерий Рейнольдса по формуле:
Найдем критерий Нуссельта по выражению:
Определим коэффициент теплоотдачи α; от ребра к окружающему воздуху по формуле:
Определим параметр ребра m по формуле:
Рассчитаем тепловой поток, передаваемый через основание ребра по формуле:
Максимальный тепловой поток, передаваемый ребром, при абсолютной теплопроводности материала ребра (λ=∞) и при температуре по всей поверхности ребра, равной температуре в его основании, определяется по выражению:
Тогда отношение действительного теплового потока к максимальному оценивает коэффициент эффективности продольного ребра прямоугольного сечения:
Для того, чтобы построить график распределения температуры по высоте ребра найдем значения температуры в точках хi=(0; 0,25∙h; 0,5∙h; 0,75∙h; h) по формуле:
Таким образом, получили следующее распределение:
Оценим вклад отвода теплоты к окружающему воздуху оребренной поверхностью по сравнению с неоребренной (ε;). Для этого найдем тепловой поток, передаваемый через всю оребренную поверхность Qоребр и поток через неоребренную поверхность плоской стенки Qнеор:
где Q – тепловой поток, передаваемый через основание ребра, (Вт); α; – коэффициент теплоотдачи от ребра к окружающему воздуху, (Вт/м2∙К).
где то тогда Следовательно, вклад отвода теплоты равен:
Дальше аналогично рассчитываем все необходимые параметры для определения распределения температуры, потока теплоты, поверхностной плотности теплового потока, коэффициента эффективности продольного ребра прямоугольного сечения в условиях вынужденного движения воздуха относительно плоской стенки (вынужденной конвекции) для оставшихся четырех высот (h) для стали, пяти высот (h) для меди при w=2 м/с. Те же расчеты проводятся для оставшихся скоростей w=6; 10; 14 м/с. Проводим оценку вклада отвода теплоты к окружающему воздуху оребренной поверхностью стенки по сравнению с неоребренной. Результаты расчета для меди и стали приведены в таблице 2.3. Таблица 2.3 – Результаты расчета передачи теплоты при вынужденной конвекции
Продолжение таблицы 2.3
Кривые зависимостей температуры от высоты ребра изображены на рисунках 2.3 – 2.11
Рисунок 2.3 – График t=f(x) при w=2 м/с (сталь)
Рисунок 2.4 – График t=f(x) при w=6 м/с (сталь)
Рисунок 2.5 – График t=f(x) при w=8 м/с (сталь)
Рисунок 2.6 – График t=f(x) при w=10 м/с (сталь)
Рисунок 2.7 – График t=f(x) при w=2 м/с (медь)
Рисунок 2.8 – График t=f(x) при w=4 м/с (медь)
Рисунок 2.9 – График t=f(x) при w=8 м/с (медь)
Рисунок 2.10 – График t=f(x) при w=10 м/с (медь)
Рисунок 2.11. График зависимости распределения температуры по высоте ребра для стали (λ1) и меди (λ2) при естественной конвекции.
2.3 Вывод Анализируя построенные графики можно сделать несколько выводов: 1. распределение температуры по высоте ребра происходит по экспоненциальному закону; 2. чем выше ребро, тем ниже температура на его конце; 3. чем больше коэффициент теплопроводности материала ребра, тем меньше разность температур в основании и на конце его, т.е. ребро пропускает больше теплоты; 4. при увеличении высоты ребра уменьшается коэффициент его эффективности, т.е. чем выше ребро, тем дальше оно от идеального (λ=∞); 5. ребро тем ближе к идеальному, чем лучше его теплопроводные свойства. Часть, тепла отводимая ребром частично тратится на собственное нагревание; 6. с увеличением скорости внешнего потока воздуха падает эффективность оребрения; 7. при увеличении скорости потока воздуха обдувающего ребро экспонента распределения температуры по высоте ребра становится более пологой, т.е. температура на конце ребра резко понижается. Увеличивается теплоотвод. 8. Вклады в отвод тепла с поверхности плоской стенки медного, латуниевого и стального оребрения при свободной и вынужденной конвекции практически одинаковы, не смотря на разные теплопроводные свойства этих материалов. Это обусловлено двумя причинами: - ребра на столько тонкие, что теплопроводные свойства материалов ребер становятся идентичными; - ребра не успевают передавать тепло. Их теплопередача максимальна уже при развитом тепловом турбулентном потоке при свободной конвекции, поэтому внешний вынужденный воздушный поток на теплоотдачу ребер слабо влияет. В качестве материала для теплоотводчиков лучше всего использовать медь. Замечание: при свободной конвекции тепло отводится больше, чем при вынужденной со скоростью воздушного потока w=2 м/с, потому что в этом случае развивается мощный тепловой поток, скорость которого больше 2 м/с.
3. Конвективный теплообмен при плёночной конденсации пара
Задание. Исследовать влияние параметров состояния пара, его скорости движения, диаметра трубки на коэффициент теплообмена при плёночной конденсации пара для вертикального и горизонтального расположения трубки. В расчётах учесть коридорную и шахматную компоновку трубок в пучке, эффект от повышения давления пара, степени паросодержания и перегрева пара, зависимость физических параметров теплоносителя от температуры, содержания воздуха в паре, волновой характер течения конденсатной плёнки, а также особенности теплообмена при вертикальном и горизонтальном расположении труб. Оценить возможность применения конденсатоотводчиков на поверхности вертикально располагаемых трубок. Рассчитать среднее значение коэффициентов теплообмена, потоки теплоты и количество конденсирующегося пара на поверхностях труб в пучке. Данные к заданию приведены в таблице.
Таблица 3.1 - Исходные данные к выполнению задания
4.1 Расчёт
Коэффициент теплообмена при конденсации пара рассчитывается через критерий Нуссельта, который в свою очередь вычисляется через критерии Архимеда или Галилея, Прандтля и Кутателадзе. Критерий Архимеда для вертикальной трубы вычисляется по формуле:
Критерий Галилея принимают вместо критерия Архимеда, если плотность пара не соизмерима с плотностью конденсата:
Для случая горизонтальной трубы вместо h в формуле принимаем d трубы. Критерий Кутателадзе:
λ – коэффициент теплопроводности жидкости, Вт/м*К ρ' и ρ" – плотность жидкости и сухого насыщенного пара, кг/м3 r – удельная теплота фазового перехода, Дж/кг ν – коэффициент кинематической вязкости жидкости, м2/с h – высота вертикальной стенки, м tc – температура стенки, 0С d – диаметр трубы, м
По полученным значениям критериев можно вычислить критерий Нуссельта для вертикальной трубы по формуле:
Критерий Нуссельта для горизонтальной трубы вычисляется по формуле:
По полученным значениям критерия Нуссельта вычислим среднее значение коэффициента теплообмена при конденсации сухого насыщенного пара на трубе.
Таблица 3.2 - Влияние давления на коэффициент теплообмена
|

 Плита толщиной s, выполненная из однородного материала и ограниченная плоскопараллельными поверхностями, по размерам много большими s, подвергается внезапному тепловому воздействию с обеих сторон потоком пара. Считая, что процесс нагрева плиты идёт по обе стороны, то начало координат целесообразно поместить в середине плиты по толщине (рисунок 1.1).
Плита толщиной s, выполненная из однородного материала и ограниченная плоскопараллельными поверхностями, по размерам много большими s, подвергается внезапному тепловому воздействию с обеих сторон потоком пара. Считая, что процесс нагрева плиты идёт по обе стороны, то начало координат целесообразно поместить в середине плиты по толщине (рисунок 1.1). (1.1)
(1.1)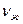 - коэффициент кинематической вязкости водяного пара, м2/с.
- коэффициент кинематической вязкости водяного пара, м2/с. - при температуре t0=120 °C;
- при температуре t0=120 °C; - при температуре t0=150 °C.
- при температуре t0=150 °C. (1.2)
(1.2) - при температуре t=120 С;
- при температуре t=120 С; - при температуре t=150 °C;
- при температуре t=150 °C;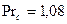 - при температуре t=100 °C.
- при температуре t=100 °C. от потока пара к поверхности плоской стенки
от потока пара к поверхности плоской стенки 
 , (1.3)
, (1.3) - коэффициент теплопроводности потока пара;
- коэффициент теплопроводности потока пара;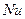
 , (1.4)
, (1.4) – коэффициент теплопроводности материала плиты, Вт/(м·К).
– коэффициент теплопроводности материала плиты, Вт/(м·К). . (1.5)
. (1.5) , (1.6)
, (1.6) - температурный напор на стенке плиты,
- температурный напор на стенке плиты, при 120 оС,
при 120 оС, при 150 оС;
при 150 оС; - начальный температурный напор,
- начальный температурный напор, при 120 оС,
при 120 оС, при 150 оС.
при 150 оС. , (1.7)
, (1.7) , м2/с.
, м2/с. (1.8)
(1.8) (1.9)
(1.9) .
. (1.10)
(1.10)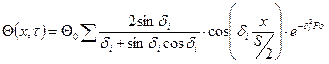 , (1.11)
, (1.11)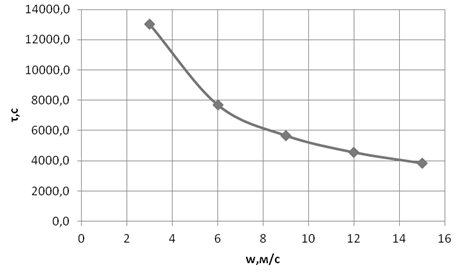






 , м
, м
 (2.1)
(2.1)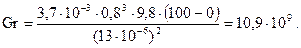
 (2.2)
(2.2) (2.3)
(2.3)
 (2.4)
(2.4)
 (2.5)
(2.5)
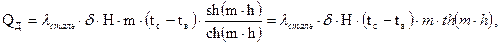 (2.6)
(2.6)
 (2.7)
(2.7)
 (2.8)
(2.8)
 (2.9)
(2.9)
 (2.10)
(2.10) (2.11)
(2.11)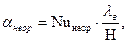 а
а (2.12)
(2.12)
 то
то (2.13)
(2.13)
 тогда
тогда и
и 
 (2.14)
(2.14)
 (2.15)
(2.15)
 (2.16)
(2.16)
 (2.17)
(2.17)
 (2.18)
(2.18)
 (2.19)
(2.19)




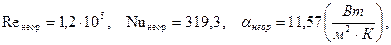
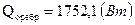 и
и 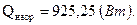










 (4.1)
(4.1) (4.2)
(4.2) (4.3)
(4.3)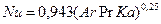 (4.4)
(4.4) (4.5)
(4.5)
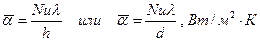 (4.6)
(4.6)


