Детерминированное моделирование, типы факторных систем и их преобразования
Одной из задач факторного анализа является моделирование взаимосвязей между результативными показателями и факторами, которые определяют их величину. Сущность моделирования заключается в том, что взаимосвязь исследуемого показателя с факторными выражается в форме конкретного математического уравнения. В детерминированном анализе выделяют следующие типы наиболее часто встречающихся факторных моделей. 1. Аддитивные модели: Они используются в тех случаях, когда результативный показатель представляет собой алгебраическую сумму нескольких факторных показателей. 2. Мультипликативные модели: Этот тип моделей применяется тогда, когда результативный показатель представляет собой произведение нескольких факторов. 3. Кратные модели: Они используются тогда, когда результативный показатель получают делением одного фактора на величину другого. 4. Смешанные (комбинированные) модели – это сочетание в различных комбинациях предыдущих моделей:
Моделирование мультипликативных факторных систем в АХД осуществляется путем последовательного расчленения факторов исходной системы на факторы-сомножители. Например, при исследовании процесса формирования объема производства продукции можно применять такие детерминированные модели, как:
Эти модели отражают процесс детализации исходной факторной системы мультипликативного вида и расширения ее за счет расчленения на сомножители комплексных факторов. Аналогичным образом осуществляется моделирование аддитивных факторных систем, т.е. путем расчленения факторов исходной модели на составные элементы. Как известно, объем реализации продукции равен:
где V ВП – объем производства; Онп – остатки нереализованной продукции. Часть нереализованной продукции может находиться на складах предприятия (Оскл), а часть может быть отгружена покупателям, но еще не оплачена (Оотг). Тогда приведенную исходную модель можно записать следующим образом:
К классу кратных моделей применяют следующие способы их преобразования: удлинения, расширения и сокращения. Метод удлинения предусматривает удлинение числителя исходной модели путем замены одного или нескольких факторов на сумму однородных показателей. Например, себестоимость единицы продукции можно представить в виде функции двух факторов: изменение суммы затрат (З) и объема выпуска продукции (V ВП). Исходная модель этой факторной системы будет иметь вид:
Если общую сумму затрат (З) заменить отдельными их элементами, такими, как оплата труда (ОТ), сырье и материалы (СМ), амортизация основных средств (А), накладные расходы (НР) и др., то получим аддитивную модель с новым набором факторов:
где х 1 – трудоемкость продукции; х 2 – материалоемкость продукции; х 3 – фондоемкость продукции; х 4 – уровень накладных затрат. Метод расширения предусматривает расширение исходной факторной модели путем умножения числителя и знаменателя дроби на один или несколько новых показателей. Например, если в исходную модель Y = a:b ввести новый показатель c, то модель примет вид:
В результате получается конечная мультипликативная модель в виде произведения нового набора факторов. Этот способ моделирования широко применяется в анализе. Например, среднегодовую выработку продукции одним работником (показатель производительности труда) можно записать таким образом:
где ДВ – среднедневная выработка; Д – количество отработанных дней одним работником. Метод сокращения представляет собой создание новой факторной модели путем деления числителя и знаменателя дроби на один и тот же показатель. В данном случае получается конечная модель того же типа, что и исходная, однако с другим набором факторов. Как известно, рентабельность совокупных активов предприятия рассчитывается делением суммы прибыли (П) на их среднегодовую величину (А);
Если числитель и знаменатель разделим на выручку (товарооборот), то получим кратную модель, но с новым набором факторов: рентабельности продаж и капиталоемкости продукции:
Процесс моделирования факторных систем – очень сложный и ответственный момент в АХД. От того, насколько реально и точно созданные модели отражают связь между исследуемыми показателями, зависят конечные результаты анализа.
|

 .
. .
. .
.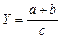 ;
;  ;
;  ;
;  и т.д.
и т.д.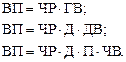
 ,
, .
. .
.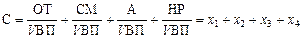 ,
, .
. . Если ввести такой показатель, как количество отработанных дней всеми работниками (Добщ), то получим следующую модель годовой выработки:
. Если ввести такой показатель, как количество отработанных дней всеми работниками (Добщ), то получим следующую модель годовой выработки: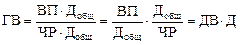 ,
,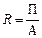 .
.
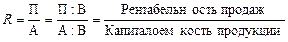 .
.


