вещественным линейным пространством
Комплексным линейным пространством 1 нет 2 нет, Является ли множество C всех комплексных чисел: Вещественным линейным пространством Комплексным линейным пространством 1 нет 2 да, Является ли множество всех целых чисел: Вещественным линейным пространством Комплексным линейным пространством 1 нет 2 да, Является ли множество всех рациональных чисел: Вещественным линейным пространством Комплексным линейным пространством 1 нет 2 да, Каким должно быть число a, чтобы множество, состоящее из одного числа, являлось линейным пространством а – любое натуральное, Является ли множество всех линейных функций одного переменного с вещественными коэффициентами Вещественным линейным пространством Комплексным линейным пространством 1 нет 2 да, Является ли множество всех многочленов от одного переменного второй степени с вещественными коэффициентами Вещественным линейным пространством Комплексным линейным пространством 1 да 2 нет, Является ли множество всех алгебраических многочленов от одного переменного не выше второй степени с вещественными коэффициентами Вещественным линейным пространством Комплексным линейным пространством 1 нет 2 да, Является ли множество всех алгебраических многочленов от одной переменной с комплексными коэффициентами комплексным линейным пространством Степени не выше Степени n Степени выше n 1 нет 2 нет 3 нет, Является ли множество всех вещественных матриц размерам mxn Вещественным линейным пространством Комплексным линейным пространством 1 нет 2 нет, Является ли множество всех комплексных матриц размеров mxn Вещественным линейным пространством Комплексным линейным пространством 1 нет 2 да, Является ли множество всех вещественных диагональных матриц порядка n: Вещественным линейным пространством Комплексным линейным пространством 1 нет 2 нет, Является ли подпространствами линейного вещественного пространства всех вещественных чисел: Множество всех четных чисел Множество всех нечетных чисел Множество всех целых чисел 1 да 2 да 3 да, Является ли множество всех вещественных чисел подпространством: Линейного вещественного пространство всех комплексных чисел Линейного комплексного пространство всех комплексных чисел 1 нет 2 нет, Является ли подпространством линейного вещественного пространства всех вещественных матриц порядка n: Множество всех вещественных невырожденных матриц порядка n Множества всех вещественных диагональных матриц порядка n 1 да 2 нет, Выяснить является ли линейного – независимой каждая из систем векторов: X 2) 1, x, x2, 2x2+3 1 нет 2 нет, Выяснить является ли линейного – независимой каждая из систем векторов: 1) 1, x, x2 2) 1, (x-2), (x-2)2 1 нет 2 да, Выяснить является ли линейного – независимой каждая из систем векторов: X 2) 1, (x-2), (x-2)2 1 нет 2 да, Выяснить является ли линейного – зависимой каждая из следующих систем векторов: 1) [1000], [0100] 2) [1000], [0100], [0010], [0001] 1 нет 2 да, Выяснить является ли линейного – зависимой каждая из следующих систем векторов: 1) [1000], [0100] 2) [1111], [0231], [004-5], [0007] 1 нет 2 да, Выяснить является ли линейного – зависимой каждая из следующих систем векторов: 1) [1000], [0100], [0010] 2) [1000], [2000], [1234] 1 да 2 да, Выяснить является ли линейного – независимой каждая из следующих систем векторов: 1) 2) 1 нет 2 нет, Выяснить является ли линейного – независимой каждая из следующих систем векторов: 1) 2) 1 нет 2 нет, Выяснить является ли линейного – независимой каждая из следующих систем векторов: 1) 2) 1 нет 2 да, Выяснить является ли линейного – независимой каждая из следующих систем векторов: 1) 2) 1 нет 2 да, Выяснить является ли линейного – независимой каждая из следующих систем векторов: 1) 2) 1 нет 2 да,
Тест 1 1. Какая из функций является четной: 1) 2. Найти точки разрыва для функции 3. Если 4. 3 вектора компланарны, если …: Лежат в одной плоскости. 5. Найти производную функции 6. Найти производную функции 7. Для 8. Найти общее решение дифференциального уравнения 9. Решить дифференциальное уравнение 10. Найти 11. Вычислите 12. Найти сумму ряда 13. Написать формулу общего члена ряда 14. Порядок дифференциального уравнения 15. Найдите формулу с помощью которой находится число сочетаний из n элементов по k элементов. 16. Вероятность появления пяти очков равна 17. Вычислите модуль числа 18.Найти значение выражения 19. Вычислить, z(2;1) если 20. Найти частную производную 21. Какое из уравнений является уравнением прямой с угловым коэффициентом?: 22. Какая прямая перпендикулярна прямой y=-2x+7: y=1/2x-7. 23. Обратная матрица 24. 25. Вычислите определитель:
Тест 2 1. Найти точки разрыва для функции 2. Найдите область определения функции 3. Нулевой вектор – это вектор …: Начало и конец которого совпадают. 4. Если вектора 5. Найти формулу с ошибкой: 6. Найти производную 7. Для 8. Решить дифференциальное уравнение 9. Укажите общий вид функции специальной правой части, линейного дифференциального уравнения с постоянными коэффициентами, к которому применим метод неопределенных коэффициентов: 10. Правая часть уравнения 11. Вычислить площадь плоской фигуры D, ограниченной заданными линиями: D: 12. Найдите интеграл ∫cos3xdx: 13. Найти 4 первых члена ряда 14. Исследовать сходимость ряда 1,1 –1,01 + 1,001 – 1,0001 + …: расходится. 15. Найдите формулу с помощью которой находится число перестановок из n элементов: 16. Из слова «великан» случайным порядком выбирают букву. Какова вероятность, что выбранной окажется гласная буква: 17. Вычислите 18. Вычислите модуль числа 19. Найти частную производную 20. Найти область определения функции 21. Указать взаимное расположение двух прямых 22. Общее уравнение плоскости имеет вид: 23. Вычислить определитель: 24. Рангом матрицы называется...: Наибольший порядок миноров, отличных от нуля. 25. Единичной матрицей является матрица...:
Тест 3
1. Найти 2. Какой предел называется первым замечательным пределом?: 3. Направляющие косинусы вектора 4. Координатная форма скалярного произведения 5. Найти производную 6. Найти формулу с ошибкой: 7. Найти вторую производную функции 8. Дифференциальным уравнением с разделяющимися переменными: Уравнением Бернулли 9. 10. Решить уравнение у// = х: 11. Найти длину дуги кривой y=f(x) от точки А(а;b) до точки В(c:d): 12. Вычислить площадь плоской фигуры D, ограниченной заданными линиями: D: 13. Гармонический ряд имеет формулу общего члена: 14. Написать формулу общего члена ряда 15. 2 стрелка стреляют по очереди. Вероятность попадания в цель первого стрелка 0,8, второго – 0,7. Найти вероятность попадания хотя бы одного стрелка. 0,94 16. Бросают 2 монеты. Чему равна вероятность появления хотя бы одного герба? 0,75 17. Указать тригонометрическую форму числа 18. Найти квадратный корень числа 19. Найти grad( 20. Дана функция 21. Какая из данных точек лежит на эллипсе 22. Какое из уравнений эллипса имеет a=4; b=3?: 23. Вычислить определитель 24. Найти произведение 25. Матрица Тест 4 1. Укажите в какой точке и какого типа функция у = 2. Вычислить предел 3. Найти вектор 4. Разложите вектор 5. Найти 6. Найдите область определения функции 7. Найдите промежутки убывания функции 8. Порядок дифференциального уравнения 9. Решите уравнение: 10. Какой подстановкой однородное дифференциальное уравнение первого порядка приводится к уравнению с разделяющимися переменными: 11. Вычислить площадь, ограниченной параболой 12. Значение определенного интеграла 13. Найдите область сходимости степенного ряда 14. Применяя признак Даламбера, исследовать ряд на сходимость 15. Всхожесть семян некоторого растения составляет 70 %. Какова вероятность того, что из 3 посеянных семян взойдут 2? ≈ 0,441. 16. По какой формуле вычисляется математическое ожидание дискретной случайной величины: 17. Вычислить 18. Найти 19. f (x,y)= 20. Функция 21. Написать каноническое уравнение параболы, если ее фокус F (6,0), а вершина в начале координат: у2 = 24х. 22. Уравнение плоскости, проходящей через точку А (-3,4,-2) и перпендикулярно вектору 23. Найдите алгебраическое дополнение 24. Чему равен ранг единичной матрицы n–го порядка? n 25. Какая система называется определенной? если имеет единственное решение.
|

 ,
, 
 ,
, 
 ,
,  ,
, 
 ,
, 
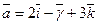 ,
,  ,
, 
 ,
, 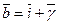
 ,
, 
 2)
2)  3)
3)  4)
4) 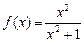 : 1 и 4
: 1 и 4 :
:  .
. , то вектора
, то вектора 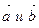 , удовлетворяющие условию
, удовлетворяющие условию  : Со направлены.
: Со направлены.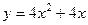 в точке x=2: 20.
в точке x=2: 20. в точке
в точке  : 0.
: 0. найдите значение производной в точке x=0: 0.
найдите значение производной в точке x=0: 0. :
:  .
. :
:  .
.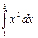 : 20
: 20 :
:  .
.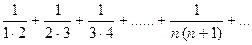 : 1.
: 1. :
:  .
.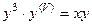 равен: 5.
равен: 5. .
. . Найти вероятность не появления пяти очков.
. Найти вероятность не появления пяти очков.  .
.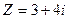 : 5.
: 5.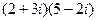 :
:  .
.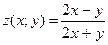 :
:  .
. , если
, если  :
:  .
.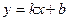 .
. к данной матрице
к данной матрице  размерности
размерности  существует, если:
существует, если:  .
.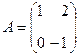 Найти
Найти  , в ответе указать сумму элементов: матрицы: 2.
, в ответе указать сумму элементов: матрицы: 2. : 0.
: 0. : 2.
: 2. :
: 
 , найти вектор
, найти вектор  :
:  .
.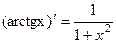 .
. :
:  .
. найдите значение производной в точке x=1: 0.
найдите значение производной в точке x=1: 0. :
: 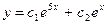 .
. .
. имеет вид
имеет вид  , где
, где  -многочлен n-й степени. В каком виде нужно искать частное решение, если число a не является корнем характерного уравнения.
-многочлен n-й степени. В каком виде нужно искать частное решение, если число a не является корнем характерного уравнения.  .
. ,
,  :
: 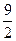 .
. sin3x+C.
sin3x+C. :
:  .
. .
. .
.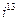 :
:  .
. :
: 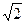 .
. : Плоскость ОХ с выколотой точкой (0;0).
: Плоскость ОХ с выколотой точкой (0;0). и
и  . взаимно перпендикулярны.
. взаимно перпендикулярны. .
. : 0.
: 0. .
. : 3/2.
: 3/2. .
.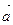 , удовлетворяют условию:
, удовлетворяют условию:  .
. при
при  имеет вид:
имеет вид:  .
. :
: 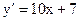 .
. .
. :
:  .
.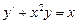 . Данное уравнение является: Линейным дифференциальным уравнением
. Данное уравнение является: Линейным дифференциальным уравнением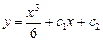
 .
.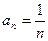 .
. :
:  .
. :
: 
 :
: 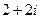
 ) в точке М(1;2):
) в точке М(1;2): 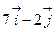 .
.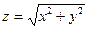 .Найти grad в точке М(3; 4):
.Найти grad в точке М(3; 4):  .
. ?: (2; 1).
?: (2; 1). .
. : 0.
: 0. :
:  .
.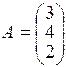
 Найти АB:
Найти АB:  .
. претерпевает разрыв: х = - 2 – точка разрыва второго рода.
претерпевает разрыв: х = - 2 – точка разрыва второго рода. : 0,5.
: 0,5. :
: 
 по векторам
по векторам  и
и  :
: 
 , если
, если 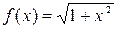 : 1
: 1 :
: 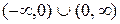
 : (0;2)
: (0;2) равен: 2.
равен: 2. :
:  .
.
 и осью абсцисс:
и осью абсцисс: 
 равно: 4.
равно: 4. : [-1, 1]
: [-1, 1] :
: 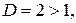 расходится
расходится
 : 2i.
: 2i.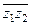 , если z1 = 3 – 4i, z2 = 1 + 3i: 15 – 5i.
, если z1 = 3 – 4i, z2 = 1 + 3i: 15 – 5i. . Найти
. Найти  0.
0. в точке (0;0): Не имеет экстремума.
в точке (0;0): Не имеет экстремума.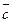 = (1,-2,3) есть: x – 2y + 3z + 17 = 0.
= (1,-2,3) есть: x – 2y + 3z + 17 = 0. элемента
элемента  определителя третьего порядка
определителя третьего порядка  : -22
: -22


