Замечательные точки и линии в треугольникеТочка пересечения медиан треугольника– центр тяжести. Точка пересечения высот – ортоцентр. Точка пересечения биссектрисс – центр вписанной окружности. Точка пересечения серединных перпендикуляров – центр описанной окружности. Медианы, проведенные из вершин A, B, C соответственно: ma, mb, mc
Разбиение треугольника медианами:
Высоты, проведенные из вершин A, B, C соответственно: ha, hb, hc
Биссектрисы, проведенные из вершин A, B, C соответственно: la, lb, lc
Свойство биссектрисы треугольника:
Формулы площади треугольника
Формула Герона: Прямоугольный треугольник
где CD = hc - высота, опущенная на гипотенузу, Подобия в прямоугольном треугольнике:
Правильный треугольник p= 3 a/ 2;
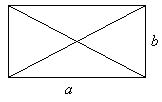
Четырехугольники Обозначения: S – площадь, R – радиус описанной окружности, r – радиус вписанной окружности, d – диагональ. Квадрат S = a 2;
Прямоугольник p=a+b (p - полупериметр) S=ab Параллелограмм p=a+b (p - полупериметр)
Ромб
М лежат на прямой, проходящей через точку пересечения диагоналей О и точку пересечения продолжений боковых сторон.
2. Средняя линия трапеции параллельна основаниям и равна их полусумме.
|
. 
;
;
. 
; 
.
. 
.
; 
;
; 
;
.
.
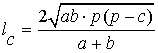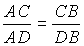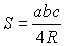Соотношения между элементами:
; 
;
;
; 
;
;
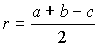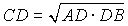или 
,
.
: 
: 
;
: 
;
.
;
; 
; 
.
.
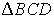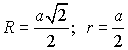
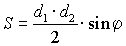
9.2.6. Трапеция
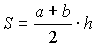
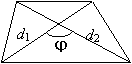
Свойства трапеции:
.
