ФОРМУЛЫ СОКРАЩЕННОГО УМНОЖЕНИЯ
СТЕПЕНИ И КОРНИ
Показательные неравенства:
КВАДРАТНЫЕ УРАВНЕНИЯ
Корни уравнения: Формулы Виета: где x 1 и x 2 – корни квадратного уравнения. Разложение квадратного трехчлена на множители:
Приведенное уравнение: Квадратное неравенство: если D >0, a >0,
где ПРОГРЕССИИ Арифметическая прогрессия: Общий член:
Частичная сумма: Геометрическая прогрессия: Общий член:
Частичная сумма: Сумма бесконечно-убывающей геометрической прогрессии (при Некоторые суммы:
ЛОГАРИФМЫ Логарифм числа
Основное логарифмическое тождество: Свойства логарифмов:
Десятичные логарифмы Натуральные логарифмы Логарифмическое неравенство:
ТРИГОНОМЕТРИЯ Основные соотношения
7.2. Перевод из радианной меры углов в градусную и обратно:
Основные значения тригонометрических функций
Знаки тригонометрических функций
Формулы сложения
Формулы двойных углов
Формулы тройных углов
Формулы половинных углов
Универсальная тригонометрическая подстановка, используемая для решения тригонометрических уравнений:
Формулы приведения
Формулы преобразования суммы и разности
|
;
;
;
;
;
;
;
; 
; 
; 
; 
; 
; 
; 
; 
; 
; 
;
.
; 
.
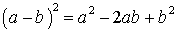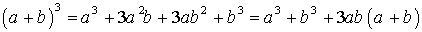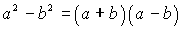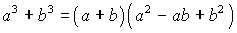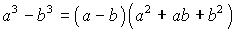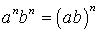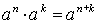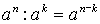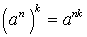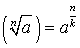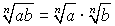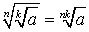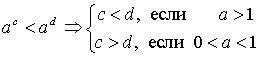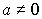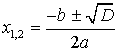, где 
- дискриминант.
; 
,
.
; 
.
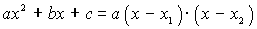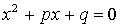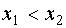, то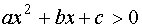
- “решение за корнями”
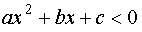
- “решение между корнями”,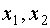
- корни квадратного трехчлена.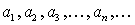
, 
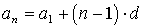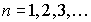, где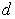 
- разность прогрессии;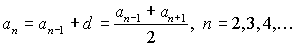
.
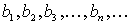
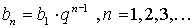, где 
- знаменатель прогрессии;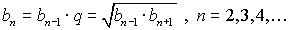
.
): 
.
; 
;
;
; 
;
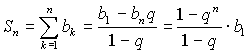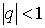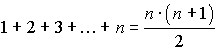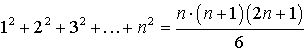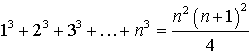по основанию 
:
.
.
; 
;
; 
; 
.
: 
.
: 
.
.
; 
; 
;
; 
; 
;
; 
.
; 
;
;
;
;
;
; 
;
; 
;
;
;
; 
;
; 
;
; 
;
; 
;
; 
;
;
; 
; 
; 
;
;
;
;
;
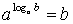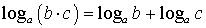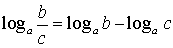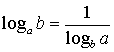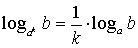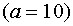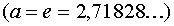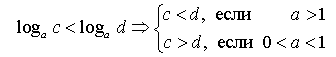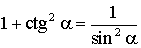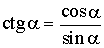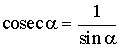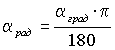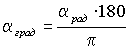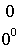
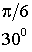
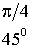
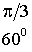
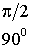
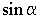
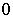
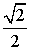
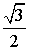
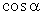
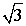
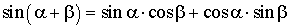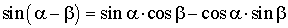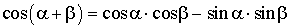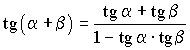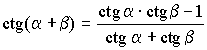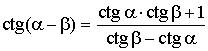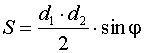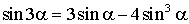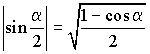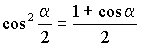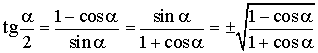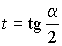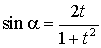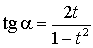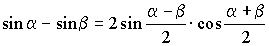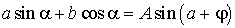, где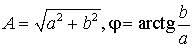 
;
; 
;
; 
.
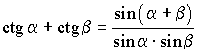