Теоретические сведения. Комбинаторикой называется раздел математики, в котором решаются задачи на составление различных комбинаций из конечного числа элементов и подсчет всех
Комбинаторикой называется раздел математики, в котором решаются задачи на составление различных комбинаций из конечного числа элементов и подсчет всех возможных таких комбинаций. 1. Правило суммы. Если множества A и B конечны и A ∩ B = Ø, то n(A ∪ B) = n(A) + n(B). Если два множества пересекаются, то количество элементов в их объединении можно найти по формуле: n(A ∪ B) = n(A) + n(B) − n(A ∩ B). 2. Правило произведения. Если из множества A элемент можно выбрать n(A) = k способами, а из множества B (непересекающегося с A) элемент можно выбрать n(B) = m способами,то упорядоченную пару (a, b) (где a ∈ A, b ∈ B) можно выбрать k · m способами. Пусть M - конечное множество, состоящее из m элементов, f: M → {1, 2,...,m} - функция, задающая порядок на M. Тогда пару (M, f) назовем упорядоченным множеством, или перестановкой из m элементов. Число таких функций на множестве из n элементов называется числом перестановок из n элементов, обозначается Pn и равно Pn = n! (1.1)
Перестановки с повторением. Рассмотрим n элементов m различных типов (m ≤ n), причем в каждом типе все элементы одинаковы. Тогда перестановки из всех этих элементов с точностью до порядка следования однотипных элементов называются перестановками с повторением. Если ni - количество элементов i-го типа (т. е.
Очевидно, в случае когда m = n, т. е. имеется по одному представителю каждого сорта, все ni = 1, и формула (1.2) переходит в (1.1). Размещением из n элементов по m называется упорядоченное подмножество, содержащее m элементов всего множества, состоящего из n нетождественных элементов. Число размещений m элементов из n возможных (0 ≤ m ≤ n) обозначается
Размещением с повторениями из n элементов по m называется упорядоченное множество, содержащее m элементов всего множества, состоящего из n нетождественных элементов,причем в подмножестве m элементов может быть произвольное число клонов каждого элемента всего множества, поэтому соотношение между m и n может быть произвольным. Число размещений с повторениями m элементов из n возможных (0 ≤ m ≤ n) обозначается Если каждый элемент всего множества, состоящего из n нетождественных элементов, обозначить своим символом, например соответствующей цифрой n-значного алфавита, то
Сочетанием из n элементов по m называется (неупорядоченное) подмножество, содержащее m элементов множества, состоящего из n нетождественных элементов. Число сочетаний из n элементов по m обозначается
Таблица 1. Элементы комбинаторики.
|

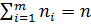 ), то число перестановок с повторением равно
), то число перестановок с повторением равно (1.2)
(1.2)
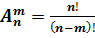 (1.3)
(1.3) (1.4)
(1.4)
 (1.5)
(1.5) Сочетанием с повторениями из n элементов по m называется (неупорядоченное) подмножество, содержащее m элементов множества, состоящего из n элементов, в которых каждый элемент может участвовать несколько раз. Число сочетаний из n элементов по m обозначается
Сочетанием с повторениями из n элементов по m называется (неупорядоченное) подмножество, содержащее m элементов множества, состоящего из n элементов, в которых каждый элемент может участвовать несколько раз. Число сочетаний из n элементов по m обозначается  (1.6)
(1.6)






