Плоская прямоугольная система координат.
Маслов А.В., Гордеев А.В., Батраков Ю.Г. Геодезия.- М.:Недра, 1993. Дьяков Б.Н. Геодезия. Общий курс: Учеб. пособие для вузов. - Новосибирск: Изд-во Новосиб ун-та, 1993.- 171 С. Борщ-Компониец В.И. Геодезия. Маркшейдерское дело: Учеб. для вузов. - М.: Недра, 1989. - 512 с.: ил. Букринский В.А., Орлов Г.В., Самошкин Е.И. и др. Основы геодезии и маркшейдерского дела. Учеб. для иностр. студ. - М.:Недра, 1989. - 382 с.: ил. Поклад Г.Г. Геодезия: Учеб. для вузов. - М.: Недра, 1988. - 304 с.: ил. Селиханович В.Г. Геодезия: Учебник для вузов, Ч.II. - М.: Недра, 1981. - 544 с. Данилов В.В., Хренов Л.С., Кожевников Н.П. и др. Геодезия. Изд. 2-е, перераб. - М.: Недра, 1976. - 488 с.: ил. Гиршберг М.А. Геодезия. Ч.1. - М,: Недра, 1967. - 384 с. Практикумы Неумывакин Ю.К., Смирнов А.С. Практикум по геодезии: Учебное пособие.- М.: Картгеоцентр - Геодезиздат, 1995.- 315 с.: ил. Визгин А.А., Коугия В.А., Хренов Л.С. Практикум по инженерной геодезии: Учеб. пособ. для вузов. - М.: Недра, 1989. - 285 с. Баканова В.В., Карклин Я.Я., Павлов Г.К. и др. Практикум по геодезии: Учеб. пособ. для вузов. Изд. 2-е, перераб. и доп. - М.: Недра, 1983. - 456 с.: ил. Хейфец Б.С., Данилевич Б.Б. Практикум по инженерной геодезии. Изд. 2-е, перераб. и доп. - М.: Недра, 1979. - 332 с.: ил. Селиханович В.Г., Козлов В.П., Логинова Г.П. Практикум по геодезии. - М.: Недра, 1978. - 382 с. Нормативно-справочная литература Инструкция по топографической съемке в масштабах 1:5000, 1:2000, 1:1000 и 1:500 / Главное управление геодезии и картографии при СМ СССР. - М.: Недра, 1982. - 160 с. Инструкция по нивелированию I, II, III, IY классов / управление геодезии и картографии при СМ СССР. - М.: Недра, 1990. - 167 с.: ил. Условные знаки для топографических планов масштабов 1:5000, 1:2000, 1:1000 и 1:500 / Главное управление геодезии и картографии при СМ СССР. - М.: Недра, 1989. - 286 с.: ил. Сборник инструкций по производству поверок геодезических приборов / Главное управление геодезии и картографии при СМ СССР.- М.: Недра, 1988. - 77 с.: ил. Инструкция о построении государственной геодезической сети СССР/ Главное управление геодезии и картографии при СМ СССР.- М.: Недра, 1966. - 342 с.
Дополнительная литература
Проблемы цифрового картографирования территории России. Обзорная информация/ Госгисцентр. - М.: ЦНИИГАиК. - 1996. - 48 с. Проект: Федеральная целевая программа Российской Федерации "Перевод геодезического обеспечения России на спутниковые методы", М., 1996. Ащеулов В.А. Применение спутниковых навигационных систем в геодезии: Уч. пособие. - Новосибирск: НИИГАиК, 1993. - 82 с. Шеховцов Г.А. Оценка точности положения геодезических пунктов. - Москва.: Недра, 1992. - 255 с.: ил. Маслов А.В., Юнусов А.Г.6 Горохов Г.И. Геодезические работы при землеустройстве: Учебн. пособие для ВУЗов. - 2-е изд.,перераб. и доп.- М.: Недра, 1990.- 215 с. Топографо-геодезические термины. Справочник / Б.С. Кузьмин, Ф.Я. Герасимов, В.М. Молоканов и др. - М.:Недра,1989.- 261 с. Бронштейн И.Н., Семендяев К.А. Справочник по математике для инженеров и учащихся ВТУЗов. - 13-е изд., исправленное. - М.: Наука, Гл. ред. физ.-мат. лит., 1986. - 544 с. Лысов Г.Ф. Поверки и исследования теодолитов и нивелиров в полевых условиях. - М.: Недра, 1978. - 97 С. Справочник геодезиста. - М.: Недра, 1985, 1975, 1966. Коськов Б.И. Справочное руководство по съемке городов. 2-е изд., перераб. и доп. - М.: Недра, 1974. - 408 С.
Плоская прямоугольная система координат.
Положение точек земной поверхности определяется прямоугольными координатами Х и У. Оси координат в геодезии развернуты на 90 градусов по сравнению с декартовой системой координат. Счет абсцисс ведется от экватора к северу со знаком плюс. К югу — со знаком минус. Для территории нашей страны абсциссы положительны, поэтому знак перед значением абсциссы не ставится (опускается). Ординаты к востоку от осевого меридиана положительны, а к западу отрицательны. Для того, чтобы все значения ординат были со знаком плюс, счет их ведется от условного меридиана, вынесенного на запад на 500 км, т.е. осевому меридиану придается значение 500 000 м. при этом впереди значения ординаты пишут номер зоны. Исправленную таким образом ординату называют приведенной или условной,а координаты называют условными или действительными. Связь между условными координатами и их действительным значением.
Х', У' — действительные значения координат Х, У — условные значения координат.
Пример: Хм = 5 650 450, где 5 650 км, 450 м Ум = 3 250 550, где 3 — номер зоны, 250 км, 550 м. Это полные условные прямоугольные координаты точки. Полные действительные координаты: Х' = 5 650450 У' = 3 -249 450 Точка М расположена в третьей зоне в 249 км 550 м к западу от осевого меридиана (250 550 — 500 000) и к северу от экватора на удалении 5 650 км 450 м.
Координаты, в которых указываются только десятки и единицы километров и метров, называются сокращенными. Хм= 05450 Ум =50550 Они применяются при работе в пределах границ карты, плана. Система применяется при составлении планов, карт
Масштабы, их виды, точность и применение Масштаб — степень уменьшения горизонтальных проекций линий местности при изображении их на плане или карте. s/S — масштаб Виды масштабов: - численный (ч.м.) - графический Ч.м. — это правильная дробь, числитель которой есть единица, а знаменатель число, показывающее, во сколько раз горизонтальные проекции линий местности уменьшены на плане или карте. s/S = 1/S:s= 1/М, где М — знаменатель ч.м. Ч.М. — безразмерная величина, поэтому его можно использовать при измерениях в любых линейных мерах. Ч.М. применяют при определении длин линий на карте (плане) или на местности
Виды графических масштабов: — линейный (л.м.) — поперечный (трансверсальный) (п.м.) Л.М. — графическое выражение численного масштаба в виде прямой линии с делениями для отсчета расстояний. Предельная и графическая точность масштаба Горизонтальное расстояние на местности, соответствующее в данном масштабе 0,1 мм, на плане называется предельной точностью масштаба.
Влияние кривизны Земли на высоты Задача определить Δh.
Анализ: R=6371км. S=1км. Δh=8см. Допустимая разность Δh на 1км. не более 5см. Уменьшим значение S до 0,3км. S=0,3км.
Кривизну Земли на участке длиной до 300 при измерении высот можно не учитывать. Кривизна Земли не влияет на условие измерения (т.к. проекция равноугольная) и её при измерениях не учитывают. Содержание топографического плана (карты) Топографический план (карта) — уменьшенное изображение на плоскости физической поверхности Земли, построенное по определенным математическим законам и наглядно показывающее при помощи системы условных знаков размещение и связи различных предметов, а также их качественные и количественные характеристики. Главное отличие плана от карты заключается в том, что при изображении участков земной поверхности на плане горизонтальные проекции соответствующих отрезков наносят без учета кривизны Земли. При составлении карт кривизну Земли приходится учитывать. По топографическому плану могут быть решены следующие задачи: • изучение и оценка местности; • решаются различные инженерные задачи, связанные с определением: — расстояний, — углов, — площадей, — высот, — превышений, — взаимной видимости точек местности, — крутизны и виды скатов и т.д.
Разграфка и номенклатура топографических карт Топографические карты обычно составляются на множестве листов. Территория всей страны изображается на них по частям. Размеры листов карты устанавливают такой величины, чтобы ими было удобно пользоваться. Так, лист карты масштаба 1:10000 для средней полосы РФ имеет размеры примерно 50 ´ 40 см и содержит изображение участка местности площадью 20 км2. Для всей территории страны число листов карты такого масштаба превышает 1 млн. Для того чтобы можно было разобраться в таком количестве картографических материалов и быстро найти нужный лист карты определенного участка местности, разработана специальная система обозначения листов карты – номенклатура. За основу разграфки и номенклатуры листов топографических карт принята разграфка листов карты масштаба 1:1 000 000. Содержание топографической карты (плана)
Азимуты, румбы и дирекционные углы Истинный азимут ( А) — горизонтальный угол, измеряемый по ходу стрелки часов между северным направлением истинного меридиана в данной точке и направлением на предмет (направлением данной линии).
Магнитный азимут ( Am) — горизонтальный угол, измеряемый по направлению хода часовой стрелки между направлением северного конца магнитного меридиана и направлением линии местности. - может иметь значение от 0 до 360 градусов Дирекционный угол ( - может иметь значение от 0 до 360 градусов Связь между азимутами и дирекционным углом. А) между истинным азимутом и дирекционным углом (через cближение меридианов
— может иметь значение от 0 до 3 градусов ( — может иметь постоянное значение для данной точки — Б) между истинным азимутом и магнитным азимутом (через магнитное склонение - может быть восточным и западным.
- склонение - величина непостоянная, зависит ль магнитного поля Земли. Наблюдаются суточное, годовое и вековое изменения склонения - на карте приводится среднее значение склонения для центра листа карты.
В) между дирекционным углом и магнитным азимутом (через поправку направления (ПН)) ПН — угол, образованный вертикально линией координатной сетки и магнитным меридианом, представляющий собой сумму сближения меридианов и магнитного склонения.
Румб — острый угол, отсчитываемый от ближайшего направления вертикальной линии координатной сетки (северного или южного) до данного направления. Румб — изменяется от О Классификация погрешностей измерений. Свойства случайных погрешностей. Любое измерение сопровождается погрешностью. Погрешность результата измерений — это разность между измеренным и истинным (точным) значением определяемой величины. (это разность между тем, что есть и тем, что должно быть). ВВиды погрешностей: - грубые; - систематические; - случайные. Грубые — погрешности, величина которых совершенно недопустима при данных условиях измерений. Возникают вследствие просчётов, промахов, например: - просчёт количества отложений мерной ленты при измерении расстояний; - просчёт при покупках на 1, 10 руб. Грубые ошибки выявляются и устраняются избыточными измерениями. Систематические - погрешности, которые входят в каждый результат по определённому закону. Могут подразделяться на: - постоянные по знаку и величине; - переменные по знаку и величине. Причины появления систематических ошибок необходимо изучать в каждом отдельном случае. Влияние их на результат измерения должен исключаться или сводится к минимуму путём введения поправок в результат измерения. Случайные — погрешности, возникновение которых не удаётся подчинить определённым законом. Случайные погрешности неизбежны. Источники случайных ошибок: - прибор - наблюдатель - внешние условия. Уменьшение влияния случайных ошибок может быть достигнуто совершенствованием приборов, повышением квалификации. Обозначения: - точное (истинное) значение величин Х - измеренное значение величин l - случайная погрешность Свойства случайных погрешностей 1. Свойство ограниченности Случайные погрешности по абсолютной величине не могут превышать определённого предела, т.е. переходят в разряд грубых погрешностей 2. Свойство симметрии Равные по абсолютной величине положительные и отрицательные случайные 3. Свойство компенсации Среднее арифметическое из случайных погрешностей равноточных измерений одной и той же величины стремится к нулю при возрастании числа измерений. 4. Свойство плотности Малые по абсолютной величине погрешности встречаются чаще, чем большие. На основании этих свойств основаны: - способы оценки точности результатов измерений - служат основой для определения наиболее надёжных значений измеряемой величины
Мерыточности равноточных измерений. О точности измерений можно приблизительно судить по рассеиванию (разбросу) результатов измерений, чем больше расходятся между собой результаты измерений, тем ниже точность измерений. Основными мерами (характеристиками) точности измерений в геодезии являются: — средняя квадратическая погрешность; — предельная п огрешность; — относительная погрешность. Средняя погрешность — среднее арифметическое из абсолютных величин Анализ: — средние погрешности этих рядов одинаковы; — отдельные случайные погрешности в 1 ряду крупнее случайных погрешностей второго ряда; — крупные погрешности снижают точность измерений. Следовательно, средняя погрешность недостаточно чувствительна к крупным погрешностям, она сглаживает их влияние. Средняя квадратическая погрешность (С.К.П.)
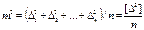
где n — число измерений. С.К.П. является надёжной мерой точности, так как она обладает тремя достоинствами: 1. На величину С.К.П. сильное влияние оказывают большие по величине погрешности, которые по существу и определяют качество измерений. 2. С.К.П. является устойчивым критерием для оценки точности измерений. 3. По величине С.К.П. можно определить предельную погрешность Выводы: 1)Исходя, из указанных достоинств С.К.П. принимается для оценки геодезических измерений в качестве основной меры точности. 2)Характеризуя точность измерения С.К.П. (m), необходимо также указывать и С.К.П. (
3)Числовые значения средней, С.К.П., и предельной погрешности достаточно вычислять до двух значащих цифр. (т = 4)Среднюю С.К.П.,
|

 Для измерения прямых координат на карты наносится координатная сетка.
Для измерения прямых координат на карты наносится координатная сетка.
 Горизонтальное расстояние на местности, соответствующее в данном масштабе 0,2 мм, на
Горизонтальное расстояние на местности, соответствующее в данном масштабе 0,2 мм, на  Такие точности измерений по каре могут быть достигнуты применением поперечного масштаба
Такие точности измерений по каре могут быть достигнуты применением поперечного масштаба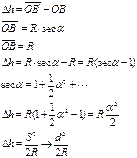


 ) — горизонтальный угол, измеряемый по направлению хода часовой стрелки между северным направлением вертикальной линии координатной сетки (осевого меридиана) и направлением данной линии местности.
) — горизонтальный угол, измеряемый по направлению хода часовой стрелки между северным направлением вертикальной линии координатной сетки (осевого меридиана) и направлением данной линии местности. )
)
 — может быть восточным и западным
— может быть восточным и западным )
) ,где
,где  =L-L0 , L0=6
=L-L0 , L0=6  *N-3
*N-3  )
)  ПН=(
ПН=( )-(
)-( ) Am=
) Am=  )
)  =l-X
=l-X
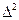 - квадрат случайной погрешности
- квадрат случайной погрешности , которая может иметь при данных условиях измерений.
, которая может иметь при данных условиях измерений. ) вычисления С.К.П.
) вычисления С.К.П.
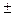 0,35 или т =
0,35 или т =  погрешность называют абсолютными погрешностями, т.к. на их значение не влияет величина измеряемой величины.
погрешность называют абсолютными погрешностями, т.к. на их значение не влияет величина измеряемой величины.


