И синтеза структуры сетей связи
Рассмотренная выше классификация сетей, а также систематизация эксплуатационных и экономических критериев и ограничений позволяют дать иерархию признаков для классификации задач анализа качества работы и синтеза структуры сетей связи. Эта иерархия содержит следующие классификационные признаки (в порядке уменьшения приоритета):
Как и следовало ожидать, тип сети здесь является главным классификационным признаком ввиду его определяющего влияния на постановку и методы решения задач анализа и синтеза. Для решения задач анализа и синтеза сетей, относящихся к большим и сложным системам, привлекается современный математический аппарат, который включает: модели и методы теории графов, методы теории вероятностей и массового обслуживания, аналитические и численные методы оптимизации, методы теории очередей, методы статистических испытаний и машинного моделирования. В настоящее время для анализа и синтеза сетей связи все шире и шире используется теория гиперсетей. Гиперсети адекватно описывают структуру сети как многослойную систему не только с горизонтальными связями, но и вертикальными системообразующими отношениями. Дальнейшее развитие теории гиперсетей будет способствовать развитию теории сетей связи и разработке методов проектирования сетей нового поколения.
12.2 Элементы математического аппарата анализа и синтеза
сети, подграфа). Под емкостью сечения понимается суммарная емкость входящих в него ветвей (ребер). Сечение с минимальной емкостью называется минимальным сечением. Для определения минимального сечения используются методы исследования потоковых графов. β ij = βji =1. При отсутствии ребра (аiаj) - βij принимает значение 0. Иногда вершинам и ребрам графа G приписываются числа, называемые весом. В зависимости от решаемой задачи в качестве весов может использоваться: длина; стоимость; пропускная способность, выраженная числом каналов или допустимой скоростью передачи информации; пропускаемая нагрузка (например, в Эрлангах) при заданном качестве обслуживания; время задержки передаваемого сообщения и т.п. В ряде случаев в качестве весов могут быть использованы: вероятности потерь вызова, надежностные показатели (например, коэффициент готовности) и т.п. Если веса присваиваются только ребрам графа, то граф называется графом c взвешенным ребрами. Если веса присваиваются только вершинам, то граф называется графом с взвешенными вершинами. Если веса присваиваются и ребрам и вершинам, то граф называется просто взвешенным графом. Для алгебраического представления графов удобно использовать следующие основные матрицы: · Структурная матрица B графа G c n узлами. Это квадратурная матрица порядка n, в которой каждому узлу ai соответствует i – ая строка и i- ый столбец: B = || bij ||. Вхождения bij определяются по следующему правилу: 1 при i = j bij = bij в случае, если есть непосредственная связь от узла ai к узлу aj. 0, если такой непосредственной связи нет. · Матрица длин ребер L = || lij ||, где lii = 0; lij – длина ребра от узла ai до узла aj; lij = ∞,если между ai и aj нет ребра. · Матрица пропускных способностей элементов сети C = || cij ||. Под пропускной способностью будем понимать либо максимальное число бит, которое может быть пропущено каналами данного ребра в единицу времени, либо обслуженную нагрузку. · Матрица прямых каналов U = || uij ||, вхождение которой uij – число каналов, начинающихся в узле ai и кончающихся в узле aj независимо от того, через какие еще транзитные или сетевые узлы эти каналы проходят. Такая матрица уже характеризует возможности сети по установлению связи, если считать, что узлы являются коммутационными. · Матрица надежности P = || pij ||, где pij – вероятность нахождения элемента сети в работоспособном состоянии. · Матрица стоимостей Ц = || цij ||, где цij – стоимость ребра между узлами ai и aj, цii – стоимость узла. В стоимость ребра может быть включена стоимость каналообразующей, а иногда и части коммутационной аппаратуры узлов ai и aj. Используя характеристики ребер и вершин графа, можно получить соответствую-щие характеристики для отдельных путей. Для пути μst = {bsl,blm, …,bpt} между вершиной s и t, содержащего ребра bsl,blm, … и bpt, в зависимости от поставленной задачи, могут быть получены различные параметры. Например: - Ранг r (μst) пути - число входящих в него ребер. - Длина пути l (μst) – сумма длин всех ребер, образующих данный путь. l (μst) = ∑ lij. b ij Є μst - Пропускная способность пути c(μst) при использовании сети для передачи инфор-мации только от узла s к узлу t определяется наиболее узким местом – минимальной пропускной способностью ребер, образующих путь. c(μst) = min c(bij). bij Є μst
- Под пропускной способностью сечения понимается суммарная емкость входящих в него ребер. Используя теорию графов можно решить множество весьма важных сетевых задач. К ним можно отнести: · Определение множества путей между любой парой узлов или путей облада-ющих определенными параметрами. Например, определить пути, ранг которых меньше или равен заданной величины. · Определение самых коротких по длине или самых надежных путей между любыми узлами графа сети. · Определение метрики графа (диаметра, медианы, радиуса), что может быть использовано при проектировании сетей связи. · Определение множества деревьев на заданном графе сети, обладающих определенными свойствами. Например, кратчайшее связывающее дерево. · Решение задачи коммивояжера, что позволяет оптимизировать первичные сети кольцевой структуры. · Определение максимальной пропускной способности некоммутируемых и коммутируемых сетей и т.п.
|


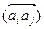 , ориентированное от ai к aj —символом
, ориентированное от ai к aj —символом 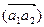 ; символ (aiaj) без стрелки будет означать, что наличие или отсутствие ориентации несущественно. Граф называется простым (некратным) и обозначается PG, если для любых ai, aj є A пучок {aiaj} содержит не более одного ребра каждого из трех возможных способов ориентации, и кратным, если это условие не выполняется. В частных случаях, когда все ребра графа ориентированы либо все ребра не имеют ориентации, граф называется, соответственно, ориентиро-ванным или неориентированным и обозначается символом
; символ (aiaj) без стрелки будет означать, что наличие или отсутствие ориентации несущественно. Граф называется простым (некратным) и обозначается PG, если для любых ai, aj є A пучок {aiaj} содержит не более одного ребра каждого из трех возможных способов ориентации, и кратным, если это условие не выполняется. В частных случаях, когда все ребра графа ориентированы либо все ребра не имеют ориентации, граф называется, соответственно, ориентиро-ванным или неориентированным и обозначается символом  или
или 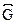 .В против-ном случае граф называется смешанным. Ориентированный граф называется симметрическим, если в нем каждому ребру
.В против-ном случае граф называется смешанным. Ориентированный граф называется симметрическим, если в нем каждому ребру 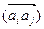 сопутствует ребро
сопутствует ребро 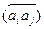 встречной ориентации, и антисимметрическим, если ребра встречной ориентации отсутствуют. Ребра
встречной ориентации, и антисимметрическим, если ребра встречной ориентации отсутствуют. Ребра 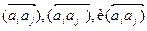 называются инцидентными узлу ai, ребро
называются инцидентными узлу ai, ребро 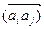 - исходящим из ai, a
- исходящим из ai, a 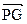 элемент этой матрицы βij принимает значение 1 только при наличии ребра
элемент этой матрицы βij принимает значение 1 только при наличии ребра 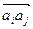 ; для графа
; для графа 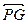 при наличии ребра (аiаj) имеем
при наличии ребра (аiаj) имеем


