Операции над логическими последовательностями
Пусть числовая последовательность системы логических функций задана в виде выражения (2.2). Рассмотрим операции над числовыми последовательностями. Их можно разделить на две группы: 1) операции над аргументами логических функций; 2) операции над самими функциями. В начале рассмотрим выполнение операций первой группы.
2.2.1. Операция подстановки значения «0» вместо аргумента с весом В результате подстановки какого-либо определённого числового значения одного из аргументов системы логических функций Утверждение 2.1. Подставить значение «0» вместо аргумента, имеющего вес Доказательство. При последовательном увеличении значения индекса Пусть, например, мы имеем следующую числовую последовательность (2.5):
Подставив значение «0» вместо аргумента с весом
Запись
2.2.2. Операция подстановки значения «1» вместо аргумента с весом Эта операция выполняется аналогично рассмотренной выше, с той лишь разницей, что процесс построения новой последовательности начинается с пропуска первых Сделав подстановку
2.2.3. Разложение числовой последовательности в матрицу по переменной с весом В результате выполнения этой операции над числовой последовательностью мы получаем числовую матрицу, имеющую две строки и Разложим, например, последовательность (2.5) по переменной с весом
Рядом c матрицей слева указывается вес переменной, по которой произведено разложение. Указанная переменная носит название выделенной переменной и изменяет своё значение с нуля на единицу по вертикали. Над матрицей указаны оставшиеся переменные, которые изменяют свои значения по горизонтали. Так как вертикальные и горизонтальные переменные взаимно дополняют друг друга до полного множества переменных, то горизонтальные переменные над матрицей можно не указывать.
2.2.4. Разложение числовой последовательности в матрицу по инверсному значению переменной с весом В результате выполнения этой операции над числовой последовательностью получается матрица с двумя строками и Разложив последовательность (2.5), например, по инверсному значению переменной с весом
2.2.5. Развёртывание матрицы разложения по переменной с весом Эта операция является обратной по отношению к разложению числовой последовательности по переменной с весом В результате развёртывания матрицы (2.6) по переменной с весом
2.2.6. Исключение из последовательности фиктивной переменной с весом Утверждение 2.2. Переменная c весом Доказательство. Для элементов числовой последовательности, находящихся в одном столбце матрицы разложения все невыделенные переменные имеют одинаковые значения. При переходе от верхнего элемента столбца к нижнему изменяет своё значение только выделенная переменная Исключение фиктивной переменной, имеющей вес Пусть, например, мы имеем числовую последовательность
Разложив её по переменной с весом
Исключив фиктивную переменную, получим следующую числовую последовательность:
В случаях, когда числовая последовательность представляет систему недоопределенных логических функций и имеет в своём составе звёздочки, для исключения фиктивной переменной строгого равенства строк матрицы разложения не требуется. Строки должны быть непротиворечивыми, то есть в одном столбце матрицы разложения не должно быть двух различных чисел. Может быть число и звёздочка или две звёздочки. Если в одном столбце имеется число и звёздочка, то в результирующей последовательности ставится на месте этого столбца число (т. е. последовательность доопределяется), а если две звёздочки, то ставится звёздочка. Пусть, например, в результате разложения по переменной с весом
Тогда после исключения фиктивной переменной мы получим последовательность
2.2.7. Введение в последовательность фиктивной переменной с весом Эта операция является обратной исключению фиктивной переменной. Выполняется она следующим образом: заданная числовая последовательность повторяется дважды одна под другой и производится развёртывание полученной матрицы по весу соответствующей входной переменной. Пусть мы имеем последовательность, определяющую функцию трёх переменных:
Необходимо в последовательность ввести фиктивную переменную, которая должна иметь вес
и развернём её по весу
Входная переменная
2.2.8. Разложение числовой последовательности по нескольким входным переменным. Пусть нам необходимо разложить некоторую числовую последовательность по двум входным переменным с весами В общем случае, если требуется разложить числовую последовательность по убывающим весам Пусть нам задана последовательность
и её требуется разложить по весам
Далее рассмотрим операции второй группы, которые выполняются над самими функциями системы.
2.2.9. Разделение числовой последовательности на старшую и младшую составляющие. Это разделение производится по весам разрядов двоичных эквивалентов чисел последовательности. Двоичный эквивалент каждого числа исходной числовой последовательности разделяется на две части относительно веса
где Пусть, например, числовую последовательность
требуется разделить на старшую и младшую составляющие относительно веса 4. Каждое число заданной числовой последовательности разделим на 4 и получим следующие две последовательности целых частей и остатков:
2.2.10. Объединение числовых последовательностей. Объединяться могут только последовательности одинаковой длины, определяющие системы логических функций от одних и тех же аргументов. Одна из последовательностей выбирается в качестве старшей, а другая – в качестве младшей. Определяется самый старший вес младшей последовательности и удваивается. С помощью найденного, таким образом веса Пользуясь операцией разделения можно из числовой последовательности системы логических функций выделить двоичную последовательность любой из составляющих эту систему логических функций. Совместно с операцией объединения операция разделения позволяет произвольным образом изменять веса двоичных последовательностей в общей числовой последовательности.
2.2.11. Логические операции над числовыми последовательностями. К числовым последовательностям можно применять все известные логические операции. Одноместная операция «НЕ» над числовой последовательностью означает поразрядную инверсию двоичного представления каждого числа последовательности. Найдём, например, инверсию последовательности (2.8). Число 6 в двоичной системе записывается как 110. Взяв, поразрядную инверсию этого кода, получим 001, то есть число 1. Число 2 записывается как 010, которое после поразрядной инверсии запишется как 101, то есть 5. И так далее. В результате получим следующую числовую последовательность:
Двухместные логические операции могут выполняться только над последовательностями одинаковой длины и определяющими системы логических функций от одних и тех же аргументов. Операция выполняется над каждой парой чисел с одним и тем же индексом В качестве примера выполним операцию «И» над последовательностями
В результате получим последовательность
|

 .
. аргументов мы получаем систему функций
аргументов мы получаем систему функций 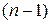 -го аргумента. При этом длина числовой последовательности, соответствующей новой системе функций сокращается вдвое, и её длинна будет равна
-го аргумента. При этом длина числовой последовательности, соответствующей новой системе функций сокращается вдвое, и её длинна будет равна  .
. , для которых двоичное представление индекса
, для которых двоичное представление индекса  имеет ноль в разряде с весом
имеет ноль в разряде с весом 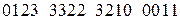 . (2.5)
. (2.5) , мы получим:
, мы получим: .
. означает, что вместо переменной c весом
означает, что вместо переменной c весом  ,
, 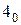 и
и  , которые теперь имеют новые весовые коэффициенты
, которые теперь имеют новые весовые коэффициенты  ,
, 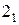 и
и  соответственно.
соответственно.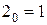 в последовательность (2.5) мы получим:
в последовательность (2.5) мы получим: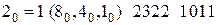 .
. в исходную последовательность, а вторая – подстановкой
в исходную последовательность, а вторая – подстановкой  .
.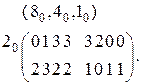 (2.6)
(2.6)
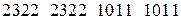 .
.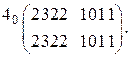
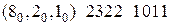 .
.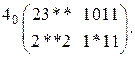
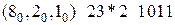 .
.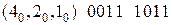 .
.
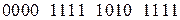 .
. , причём
, причём 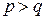 . Для осуществления рассматриваемой операции необходимо вначале построить матрицу разложения последовательности по старшей входной переменной
. Для осуществления рассматриваемой операции необходимо вначале построить матрицу разложения последовательности по старшей входной переменной  столбцов.
столбцов.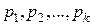 , то первые
, то первые 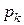 элементов последовательности помещаются в первую строку результирующей матрицы, вторые
элементов последовательности помещаются в первую строку результирующей матрицы, вторые  . После этого начинают заполняться по тому же правилу третья и четвёртая строки матрица, пока мы снова не выберем
. После этого начинают заполняться по тому же правилу третья и четвёртая строки матрица, пока мы снова не выберем 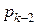 , по тому же правилу заполняются пятая, шестая, седьмая и восьмая строки матрицы.
, по тому же правилу заполняются пятая, шестая, седьмая и восьмая строки матрицы.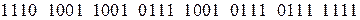
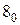 ,
, 
 . Тогда любое число
. Тогда любое число 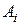 в последовательности (2.2) можно представить в следующем виде:
в последовательности (2.2) можно представить в следующем виде: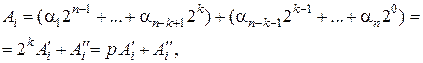 (2.7)
(2.7)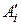 – старшая составляющая числа
– старшая составляющая числа 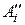 – младшая. Для того, чтобы число
– младшая. Для того, чтобы число  (2.8)
(2.8)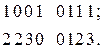
 для каждой пары
для каждой пары  и
и  по формуле (2.7) находится число
по формуле (2.7) находится число 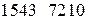 .
. .
.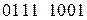 и
и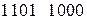 .
. .
.


