Теоретическая часть. Во всяком проводящем контуре, по которому течет ток, сила которого меняется с течением времени I(t)
Практикум по физике

Во всяком проводящем контуре, по которому течет ток, сила которого меняется с течением времени I(t), в силу явления электромагнитной индукции возникает поле сторонних сил, препятствующих изменению тока. Это явление получило название явления самоиндукции. Контур оказывается погруженным в меняющееся магнитное поле, которое он сам же и порождает. Поле сторонних сил, возникающее при этом в контуре, принято характеризовать величиной ЭДС самоиндукции Ф=LI. Таким образом,
Уравнение (1) показывает, что индуктивность контура L можно считать и коэффициентом пропорциональности между ЭДС самоиндукции и скоростью изменения силы в контуре тока. Единица измерения индуктивности 1 генри = 1 Гн = 1Вб/1А. Индуктивность зависит от геометрии контура. Индуктивность кольца радиусом 10 см из проволоки диаметром 1 мм составляет примерно 1 мкГн. Индуктивность катушек из провода с сердечником из ферромагнитного материала может достигать нескольких десятков генри. Поскольку направление возникающих в ходе явления самоиндукции электрических полей таково, что они препятствуют изменению тока, индуктивность характеризует способность контура препятствовать увеличению сила тока в контуре при его нарастании за счет внешних источников напряжения или поддерживать протекание тока, если сила тока в контуре начинает убывать. Это свойство используется в электронике и электротехнике для сглаживания пульсаций тока, поэтому важно уметь создавать технические устройства, имеющие большую индуктивность при низком омическом сопротивлении и малой емкости. Такими свойствами в значительной степени обладает соленоид – цилиндрическая катушка, длина которой намного превышает диаметр, провод которой имеет достаточно большое сечение и изготовлен из материала с малым удельным сопротивлением (например, из меди). Индуктивность соленоида зависит от материала сердечника (m - магнитная проницаемость вещества сердечника), на котором смонтирована катушка, от площади сечения катушки S или ее диаметра D и от числа витков N на единицу длины l соленоида. Для длинного (l>>D), намотанного в один слой тонкой проволокой (D>>d, где d - диаметр провода), можно пренебречь неоднородностью магнитного поля на концах соленоида и показать, что
где m0 = 4p×10-7 Гн/м - магнитная постоянная, а n=N/l. Для соленоидов конечной длины имеются более точные, но более громоздкие формулы расчетные формулы, однако на практике индуктивность соленоидов, особенно с многослойной намоткой измеряют в эксперименте. Соленоид, намотанный из реальной проволоки помимо индуктивности L обладает омическим сопротивлением RL. В цепях переменного синусоидального тока с циклической частотой w, вводят также величину Lw называемую индуктивным сопротивлением. Первый способ измерения индуктивности соленоида связан с обработкой кривой нарастания тока в цепи, содержащей соленоид с резистором с известным сопротивлением R, при замыкании соединяющего эту цепь к источнику постоянного напряжения с ЭДС равной
Рис. 1
Закон Ома для такой цепи (рис. 1, показано направление обхода) после замыкания ключа:
С учетом ЭДС самоиндукции:
Преобразуя уравнение, получим
где
где На рис. 2 показана еще одна характерная точка графика, которая может быть легко найдена после проведения эксперимента (штрих - пунктирная линия): t1/2 - время, при которой сила тока достигает половины конечного значения. Легко показать, используя свойства показательной функции, что t1/2=t×ln2»0.69t
Рис. 2
Таким образом, оценить индуктивность катушки можно, зная характерное время нарастания кривой I(t) и величину суммарного сопротивления резистора и катушки. Заметим, что сила тока в каждый момент времени пропорциональна напряжению на резисторе R (UR=IR, Uмакс=I0R), поэтому график U(t) будет иметь вид, аналогичный I(t) (рис. 2):
и характерное время t можно измерить, регистрируя зависимость напряжения на резисторе от времени после замыкания цепи. Более точное значение t можно получить, измерив Uмакс и подобрав с помощью компьютера такой коэффициент для функции Для определения L по величине Второй способ измерения индуктивности основывается на получении кривой протекания тока в цепи, содержащей резисторы и катушку, после отключения источника тока (рис. 3).
а) б) Рис.3
Поскольку при размыкании цепи сила тока в соленоиде начинает убывать, благодаря явлению самоиндукции в нем возникают сторонние силы, поддерживающие ток. Ток спадает не сразу, а некоторое время после размыкания ключа течет через катушку и резистор R2. Эту способность соленоида поддерживать некоторое время ток в цепи трактуют как наличие в нем до размыкания цепи запаса энергии. Эту энергию приписывают энергии магнитного поля, находящегося, в основном, внутри соленоида. Закон Ома для замкнутой цепи (рис. 3б, показано направление обхода) в этом случае
Это дифференциальное уравнение имеет решение (при условиях I(0)=I0 и I(¥)=0)
где
Рис. 4
Как и на рис. 2, можно показать, что характерное время t - это время, за которое ток в цепи спал бы до нуля, сохраняя начальную скорость убывания. В данном случае этому времени также можно придать смысл времени, за которое сила тока уменьшается в e»2,73 раза. Время t1/2 – время, за которое сила тока упала в 2 раза, по-прежнему связано с t соотношением t1/2=t×ln2»0.69t. Вместо измерения тока в данной лабораторной работе для определения t используется измерение напряжения на резисторе R или R2, так как напряжение на них в каждый момент времени отличается от силы тока постоянным множителем, равным сопротивлению резисторов. Так же как и в первом способе измерения индуктивности, можно определить время t, подбирая с помощью компьютера коэффициент A для функции Отметим, что ток через резистор R2 после размыкания цепи (рис. 3б) потечет в противоположную сторону по сравнению с током до размыкания. Другой станет и сила тока. Если до размыкания сила тока через резистор с сопротивлением R2, большим RL была меньше, чем I0 ( Третий способ измерения индуктивности соленоида связан с изучением соотношения амплитудного значения напряжения на соленоиде и последовательно соединенном с ним резисторе при прохождении по такой цепи синусоидального переменного тока (рис. 5). В данном случае ЭДС самоиндукции постоянно меняет свое значение, а периодически и знак.
Рис. 5
Закон Ома для полной цепи в данном случае запишется как
Учитывая, что
При синусоидальном законе изменения ЭДС генератора
или
Используя метод векторных диаграмм или преобразование тригонометрических функций, можно показать, что выполнение этого условия возможно, если амплитуды напряжений на катушке и на резисторе R2 соответственно равны:
При этом сдвиг фаз j между напряжениями на резисторе и на катушке составит
При Lw >>(
В этом случае L=kR2.
|

 . ЭДС самоиндукции, как характеристика явления электромагнитной индукции, прямо пропорциональна изменению магнитного потока, создаваемого меняющимся магнитным полем. Коэффициент пропорциональности между силой тока I, текущего в контуре, и магнитным потоком Ф, порожденным контуром и пронизывающим сам контур, называется индуктивностью контура L:
. ЭДС самоиндукции, как характеристика явления электромагнитной индукции, прямо пропорциональна изменению магнитного потока, создаваемого меняющимся магнитным полем. Коэффициент пропорциональности между силой тока I, текущего в контуре, и магнитным потоком Ф, порожденным контуром и пронизывающим сам контур, называется индуктивностью контура L: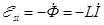 (1)
(1)
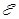 (рис.1).
(рис.1).
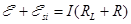 .
.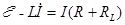 (2)
(2)

 ,
,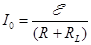 максимальная сила тока, который установится в цепи, когда он перестанет меняться и выполнится равенство
максимальная сила тока, который установится в цепи, когда он перестанет меняться и выполнится равенство 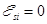 . Решение такого дифференциального уравнения при условии I(0)=0, а I(¥)=I0 выглядит следующим образом
. Решение такого дифференциального уравнения при условии I(0)=0, а I(¥)=I0 выглядит следующим образом (2),
(2),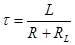 - характерное время процесса, определяемое индуктивностью катушки и общим омическим сопротивлением цепи. График такой функции показан на рис. 2. Поскольку в начальные моменты времени I»0, уравнение (1) имеет вид
- характерное время процесса, определяемое индуктивностью катушки и общим омическим сопротивлением цепи. График такой функции показан на рис. 2. Поскольку в начальные моменты времени I»0, уравнение (1) имеет вид 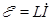 , откуда
, откуда 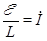 , то есть ток нарастает линейно. Проводя касательную к начальному участку на графике I(t), легко видеть, что она пересекает на прямую I(t)=I0 при t=t (пунктир на рис. 2). То есть характерное время процесса показывает, как быстро сила тока достигла бы конечного значения, если бы ток продолжал нарастать с начальным темпом.
, то есть ток нарастает линейно. Проводя касательную к начальному участку на графике I(t), легко видеть, что она пересекает на прямую I(t)=I0 при t=t (пунктир на рис. 2). То есть характерное время процесса показывает, как быстро сила тока достигла бы конечного значения, если бы ток продолжал нарастать с начальным темпом.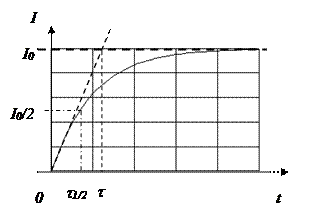
 (3)
(3) , при котором график такой функции проходит максимально близко ко всем экспериментальным точкам зависимости U(t) (по методу наименьших квадратов) [1]. В этом случае t=1/А.
, при котором график такой функции проходит максимально близко ко всем экспериментальным точкам зависимости U(t) (по методу наименьших квадратов) [1]. В этом случае t=1/А.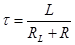 следует предварительно измерить величину RL, например, по отношению напряжений в цепи постоянного тока на последовательно соединенных соленоиде и резисторе с известным сопротивлением R (рис. 1).
следует предварительно измерить величину RL, например, по отношению напряжений в цепи постоянного тока на последовательно соединенных соленоиде и резисторе с известным сопротивлением R (рис. 1).

 или
или
 ,
,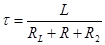 . График такой функции I(t) показан на рис. 4.
. График такой функции I(t) показан на рис. 4.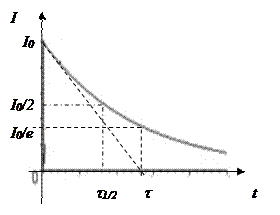
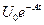 , при котором ее график спадает от начального напряжения до нуля, проходя максимально близко ко всем экспериментальным точкам зависимости U(t) (по методу наименьших квадратов) [2]. В этом случае t=1/А После этого индуктивность катушки находится из соотношения
, при котором ее график спадает от начального напряжения до нуля, проходя максимально близко ко всем экспериментальным точкам зависимости U(t) (по методу наименьших квадратов) [2]. В этом случае t=1/А После этого индуктивность катушки находится из соотношения 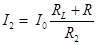 ), то после резкого размыкания в первый момент времени она будет стремиться стать равной I0, то есть возрастет в
), то после резкого размыкания в первый момент времени она будет стремиться стать равной I0, то есть возрастет в 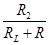 раз. Таким образом, если измерять напряжение на резисторе до и после размыкания, то оно после размыкания меняет знак и может существенно увеличивать свой модуль. При размыкании цепи в отсутствии резистора R2 (что эквивалентно условию R2 =¥) напряжение возрастает очень сильно, поэтому на контактах ключа, размыкающего цепь, может возникнуть искровой (или дуговой) разряд через воздух.
раз. Таким образом, если измерять напряжение на резисторе до и после размыкания, то оно после размыкания меняет знак и может существенно увеличивать свой модуль. При размыкании цепи в отсутствии резистора R2 (что эквивалентно условию R2 =¥) напряжение возрастает очень сильно, поэтому на контактах ключа, размыкающего цепь, может возникнуть искровой (или дуговой) разряд через воздух.

 , а напряжение на соленоиде
, а напряжение на соленоиде  , можно записать:
, можно записать: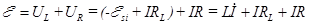
 с циклической частотой w, в цепи установятся вынужденные колебания с той же частотой. Если при этом сила тока в цепи меняется по синусоидальному закону
с циклической частотой w, в цепи установятся вынужденные колебания с той же частотой. Если при этом сила тока в цепи меняется по синусоидальному закону 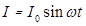 , то для любого момента времени должно выполняться соотношение:
, то для любого момента времени должно выполняться соотношение:
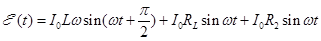
 и
и 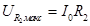

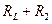 ) сдвиг фаз существенен и равен j»p/2, а при Lw<<;(
) сдвиг фаз существенен и равен j»p/2, а при Lw<<;(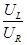 от w при RL<<Lw (эквивалентно w>>RL/L), то есть при больших частотах.
от w при RL<<Lw (эквивалентно w>>RL/L), то есть при больших частотах.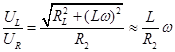 .
.


