Құбыр бойымен газдысұйық қоспасы қозғалған кезде оның қысымы арқылы газ бен сұйықтың белгілі бір мөлшері өтеді. Егерде барлық газ көбіктері құбыр қимасының негізгі бөлігін 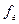 жабады деп, ал сұйық осы қиманың қалған ауданын қамтиды
жабады деп, ал сұйық осы қиманың қалған ауданын қамтиды 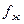 десек, онда
десек, онда  , мұнда
, мұнда  — құбырдың қима ауданы (1 сурет). ГСҚ- ның тығыздығы бұл жағдайда орташа өлшенген мәнмен анықталады
— құбырдың қима ауданы (1 сурет). ГСҚ- ның тығыздығы бұл жағдайда орташа өлшенген мәнмен анықталады
 . (1)
. (1)
мұнда,  және
және 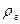 —қиманың термодинамикалық жағдайы кезіндегі сұйықтармен газдардың тығыздығы.
—қиманың термодинамикалық жағдайы кезіндегі сұйықтармен газдардың тығыздығы.
Әдетте  қатынасын
қатынасын 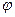 -мен белгілейді.
-мен белгілейді.
Сонда, 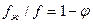 ,
,
 . (2)
. (2)
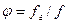 шамасын ағынның айқын базқұрамы деп атайд. Келесі көрсеткіштерді былай белгілейміз:
шамасын ағынның айқын базқұрамы деп атайд. Келесі көрсеткіштерді былай белгілейміз:
V —берілген қимадан өтетін газдың көлемдік шығыны; q -осы қимадан өтетін сұйықтық көлемдік шығыны; 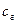 — құбыр қабырғасына қатысты газ қозғалысының сызықтық жылдамдығы;
— құбыр қабырғасына қатысты газ қозғалысының сызықтық жылдамдығы; 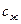 —құбыр қабырғасына қатысты сұйық қозғалысының сызықтық жылдамдығы.
—құбыр қабырғасына қатысты сұйық қозғалысының сызықтық жылдамдығы.
Онда келесі қатынастарды былай жазуға болады:
 ,
,  (3)
(3)
 . (4)
. (4)
(3) пен (4) –ті (1) – ге қоя отырып және кейбір қысқартулар жасап келесі теңдеуді аламыз:
 . (5)
. (5)
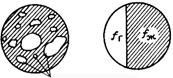
1-сурет көбіктері құбырдағы газ және сұйық алып жатқан орташа статикалық аудан.
Көтеріліп келе жатқан ағымдағы газ, сұйыққа қарағанда тез қозғалады, өйткені оған Архимед күші әсер етеді.
 , (6)
, (6)
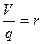 . (7) деп белгілейміз
. (7) деп белгілейміз
(5)- тегі теңдеудің алымы мен бөлімін 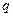 - ға бөліп және (6) мен (7)- ге сәйкес жаңа белгілеуді еңгізе отырып, келесіні аламыз:
- ға бөліп және (6) мен (7)- ге сәйкес жаңа белгілеуді еңгізе отырып, келесіні аламыз:
 , (8)
, (8)
мұнда, Г-қарастырылып отырған қимадағы термодинамикалық жағдайға келтірілген газ факторы.
 кезде
кезде 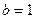 және (8) – теңдеуден мынаны аламыз
және (8) – теңдеуден мынаны аламыз
 . (9)
. (9)
Бұл жағдай идеалды жағдайға сәйкес келеді, мұнда тығыздығы 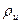 - тең идеалды қоспаны түзеді.
- тең идеалды қоспаны түзеді.
Газдың салыстырмалы жылдамдығы
(сұйыққа қатысты)
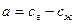 , (10)
, (10)
 . (11)
. (11)
(11) теңдігі (6)-ға қоя отырып келесіні аламыз:
 . (12)
. (12)
а>0 болса, онда b>1. Көлемдік шығын V өзгермеген кезде газ жылдамдығының ұлғаюы 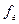 -ны азайтып, сәйкесінше
-ны азайтып, сәйкесінше 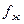 -ны ұлғайтады. Нәтижесінде қоспаның тығыздығы ұлғаяды.
-ны ұлғайтады. Нәтижесінде қоспаның тығыздығы ұлғаяды.
Осылайша көлемдік шығын өзгермген кезде газдың сырғанау көрінісі 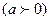 идеалды жағдаймен салыстырғанда қоспаның ауырлауына әкеледі.
идеалды жағдаймен салыстырғанда қоспаның ауырлауына әкеледі.
Сондықтан  неғұрлым үлкен болса, соғұрлым осы берілген сұйық мөлшерін көтеру үшін ұңғы түбінде қысымды көп қажет етеді.
неғұрлым үлкен болса, соғұрлым осы берілген сұйық мөлшерін көтеру үшін ұңғы түбінде қысымды көп қажет етеді.
Нақты қоспаның тығыздығы:
 , (13)
, (13)
Мұнда  - сырғанауға байланысты қоспа тығыздығының ұлғаюы
- сырғанауға байланысты қоспа тығыздығының ұлғаюы  анықтау үшін (8)-ші теңдеуге
анықтау үшін (8)-ші теңдеуге 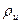 қосып және сәйкесінше (9)-дем
қосып және сәйкесінше (9)-дем 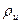 -ды алып тастаймыз, одан әрі қосындыларды топтастыра отырып, кейбір өзгертулер жасап, ортақ бөлімге келтіріп және қосындыларды қосқаннан кейін келесіні табамыз:
-ды алып тастаймыз, одан әрі қосындыларды топтастыра отырып, кейбір өзгертулер жасап, ортақ бөлімге келтіріп және қосындыларды қосқаннан кейін келесіні табамыз:
 . (14)
. (14)
(14), (13) және (9) –ды салыстыра отырып мынаны аламыз:
 . (15)
. (15)
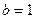 кезде
кезде  болған кезде газдың сырғанауы болмайды (15) теңдеудегі алымы нолге теңестіріледі және
болған кезде газдың сырғанауы болмайды (15) теңдеудегі алымы нолге теңестіріледі және  . Мына графиктің штрихталған бөлігі газ сырғанауы есебінен ГСҚ- ның тығыздығының ұлғаюын көрсетеді.
. Мына графиктің штрихталған бөлігі газ сырғанауы есебінен ГСҚ- ның тығыздығының ұлғаюын көрсетеді.

2сурет. Газ сырғанауы нәтижесінде болған ГСҚ-ның тығыздығының өзгеруі.
ГСҚ-ның тығыздығының теориясында мынадай түсінік бар, бұл арқылы қоспа тығыздығын анықтайды. Бұл шығындалатын газ құрамы 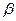 және айқын газ құрамы
және айқын газ құрамы 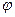 .
.
ГСҚ-ы ағынының шығындалатын газ құрамы көлемдік шығынның 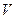 қоспаның жалпы шығынына қатынасымен анықталады
қоспаның жалпы шығынына қатынасымен анықталады 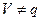
 . (16)
. (16)
ГСҚ-ы ағынның айқын газ құрамы газдың сырғанауын ескереді және сондықтан құбырдың барлық қимасының  газдың алып жатқан ауданына
газдың алып жатқан ауданына  қатынасымен сипатталады:
қатынасымен сипатталады:
 . (17)
. (17)
сонда
 . (18)
. (18)
(18) және (8) теңдеулерді салыстыра отырып мынаны аламыз:
 , (19)
, (19)
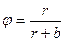 . (20)
. (20)
(16) – шы теңдеудің алымын да, бөлімін де 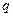 -ға бөле отырып және (7) –ші теңдеудің мәндерін қоя отырып келесіні аламыз:
-ға бөле отырып және (7) –ші теңдеудің мәндерін қоя отырып келесіні аламыз:
 . (21)
. (21)
бұдан
 . (22)
. (22)
(22)-ші, (21) –ші және (9)-шы теңдеулерді қолдана отырып мынаны аламыз:
 . (23)
. (23)
Осылайша идеалды қоспаның тығыздығы (23) шығындалатын газ құрамы мен 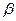 анықталады, ал реалды қысымның тығыздығы (18) –айқын газ құрамымен
анықталады, ал реалды қысымның тығыздығы (18) –айқын газ құрамымен 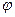 -анықталады
-анықталады
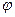 ,
, 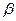 ,
,  ,
,  .арасындағы байланыстары бар формуланы табамыз:
.арасындағы байланыстары бар формуланы табамыз:
Из (20) и (21) имеем
(20) және (21) теңдеуден  . (24)
. (24)
 -ге қатысты (21)-шеше отырып мынаны табамыз:
-ге қатысты (21)-шеше отырып мынаны табамыз:
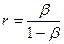 . (25)
. (25)
(24)-ті (25)-ші теңдеуге қоя отырып келесіні аламыз:
 . (26)
. (26)
 -ға қатысты (26)-шы теңдеуді шешіп мынаны аламыз
-ға қатысты (26)-шы теңдеуді шешіп мынаны аламыз
 . (27)
. (27)
ГСҚ-ң қозғалысы кезінде екі жағдай болуы мүмкін, бірінші жағдайда құбыр бойымен тек қана сұйық қозғалады 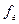 = 0, ал екінші жағдайда құбыр бойымен тек қана газ қозғалады
= 0, ал екінші жағдайда құбыр бойымен тек қана газ қозғалады 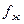 = 0.
= 0.
Идеалды көтергіш үшін 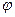 (
(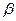 ) квадрат диагоналы түріндегі түзу сызық болып түседі (3 сурет 1 түзу сызық). b>1 кезіндегі барлық басқа жағдайларда,яғни а>0(сг>сж) кезінде
) квадрат диагоналы түріндегі түзу сызық болып түседі (3 сурет 1 түзу сызық). b>1 кезіндегі барлық басқа жағдайларда,яғни а>0(сг>сж) кезінде 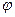 <
< 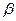 тең деп аламыз.
тең деп аламыз.
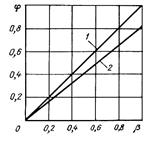
3 сурет. 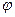 -ның
-ның 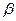 -дан тәуелділігі газ сырғанауы болмаған кезде (
-дан тәуелділігі газ сырғанауы болмаған кезде (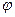 =
= 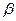 , 1 сызық) және сырғанауы болғанда (
, 1 сызық) және сырғанауы болғанда (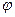 <
< 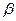 , 2 сызық)
, 2 сызық)
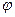 (
(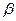 ) а, b,.
) а, b,. 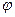 (
(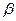 ).
).
Осн.: 1. [220-227], 3. [270-314],1. [227-229], 3. [270-314], 1. [229-242], 3. [270-314]
Контрольные вопросы:
- Газ шығынына байланысты газды сұйық көтергішінің бергіштігі қалай өзгереді?
- Көтергіш құбырды батыруға байланысты q(V) қисығының жату жағдай қалай өзгереді?
- Құбыр диаметріне байланысты q(V) қисығының жату жағдай қалай өзгереді?
- ГСҚ-сы қозғалыс процессінің ПӘК-і?
5. Тура есеп деп нені айтады?
6. Кері есеп деп нені айтады?
7. Қысым балансының теңдеуіне кіретін қысымдарды білу қажет?
8. Дифференциял түрдегі қысым қысым балансының теңдеуі қалай жазылады?
- Ағынның айқын газ құрамы деп қандай шаманы айтамыз?
- Идеалды шартқа қандай жағдай сәйкес келеді?
- Реалды қоспаның тығыздығын қалай анықтайды?
- Шығынды газ құрамын қалай анықтайды?
- Идеалды қоспаның қоспаның тығыздығын қалай анықтайды?

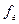 жабады деп, ал сұйық осы қиманың қалған ауданын қамтиды
жабады деп, ал сұйық осы қиманың қалған ауданын қамтиды 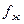 десек, онда
десек, онда  , мұнда
, мұнда  — құбырдың қима ауданы (1 сурет). ГСҚ- ның тығыздығы бұл жағдайда орташа өлшенген мәнмен анықталады
— құбырдың қима ауданы (1 сурет). ГСҚ- ның тығыздығы бұл жағдайда орташа өлшенген мәнмен анықталады . (1)
. (1) және
және 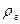 —қиманың термодинамикалық жағдайы кезіндегі сұйықтармен газдардың тығыздығы.
—қиманың термодинамикалық жағдайы кезіндегі сұйықтармен газдардың тығыздығы. қатынасын
қатынасын 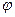 -мен белгілейді.
-мен белгілейді.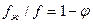 ,
, . (2)
. (2)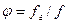 шамасын ағынның айқын базқұрамы деп атайд. Келесі көрсеткіштерді былай белгілейміз:
шамасын ағынның айқын базқұрамы деп атайд. Келесі көрсеткіштерді былай белгілейміз: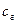 — құбыр қабырғасына қатысты газ қозғалысының сызықтық жылдамдығы;
— құбыр қабырғасына қатысты газ қозғалысының сызықтық жылдамдығы; 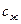 —құбыр қабырғасына қатысты сұйық қозғалысының сызықтық жылдамдығы.
—құбыр қабырғасына қатысты сұйық қозғалысының сызықтық жылдамдығы. ,
,  (3)
(3) . (4)
. (4) . (5)
. (5)
 , (6)
, (6)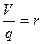 . (7) деп белгілейміз
. (7) деп белгілейміз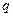 - ға бөліп және (6) мен (7)- ге сәйкес жаңа белгілеуді еңгізе отырып, келесіні аламыз:
- ға бөліп және (6) мен (7)- ге сәйкес жаңа белгілеуді еңгізе отырып, келесіні аламыз: , (8)
, (8) кезде
кезде 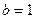 және (8) – теңдеуден мынаны аламыз
және (8) – теңдеуден мынаны аламыз . (9)
. (9)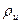 - тең идеалды қоспаны түзеді.
- тең идеалды қоспаны түзеді.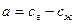 , (10)
, (10) . (11)
. (11) . (12)
. (12)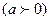 идеалды жағдаймен салыстырғанда қоспаның ауырлауына әкеледі.
идеалды жағдаймен салыстырғанда қоспаның ауырлауына әкеледі. неғұрлым үлкен болса, соғұрлым осы берілген сұйық мөлшерін көтеру үшін ұңғы түбінде қысымды көп қажет етеді.
неғұрлым үлкен болса, соғұрлым осы берілген сұйық мөлшерін көтеру үшін ұңғы түбінде қысымды көп қажет етеді. , (13)
, (13) - сырғанауға байланысты қоспа тығыздығының ұлғаюы
- сырғанауға байланысты қоспа тығыздығының ұлғаюы  . (14)
. (14) . (15)
. (15) болған кезде газдың сырғанауы болмайды (15) теңдеудегі алымы нолге теңестіріледі және
болған кезде газдың сырғанауы болмайды (15) теңдеудегі алымы нолге теңестіріледі және  . Мына графиктің штрихталған бөлігі газ сырғанауы есебінен ГСҚ- ның тығыздығының ұлғаюын көрсетеді.
. Мына графиктің штрихталған бөлігі газ сырғанауы есебінен ГСҚ- ның тығыздығының ұлғаюын көрсетеді.
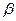 және айқын газ құрамы
және айқын газ құрамы 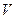 қоспаның жалпы шығынына қатынасымен анықталады
қоспаның жалпы шығынына қатынасымен анықталады 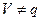
 . (16)
. (16) қатынасымен сипатталады:
қатынасымен сипатталады: . (17)
. (17) , (19)
, (19)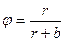 . (20)
. (20) . (21)
. (21) . (22)
. (22) . (23)
. (23) ,
,  .арасындағы байланыстары бар формуланы табамыз:
.арасындағы байланыстары бар формуланы табамыз: . (24)
. (24) -ге қатысты (21)-шеше отырып мынаны табамыз:
-ге қатысты (21)-шеше отырып мынаны табамыз: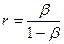 . (25)
. (25) . (26)
. (26) -ға қатысты (26)-шы теңдеуді шешіп мынаны аламыз
-ға қатысты (26)-шы теңдеуді шешіп мынаны аламыз . (27)
. (27)



