Угловая засечка.
Этот способ применяется для разбивки удаленных и труднодоступных объектов - мостовых переходов и гидротехнических сооружений. При этом, положение проектной точки P с известными координатами определяют в натуре путем построения двух проектных углов b1 и b2 соответственно в двух твердых пунктах A и B (рис. 91).
Рисунок 91 - Прямая угловая засечка На точность разбивки влияют следующие источники: погрешность собственно прямой засечки и погрешность, обусловленная неточностью фиксации линий засечки
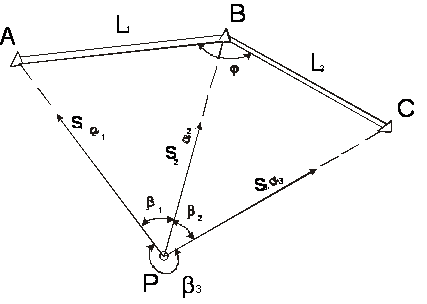
Способ применяется для уточнения положения приближенной точки сооружений при помощи измеренных на ней горизонтальных углов b1, b2, b3 на три опорные пункта (рис. 94) с последующим редуцированием (при разбивке центров мостовых опор, бычков плотин и других сооружений).
Рисунок 94 - Обратная засечка Погрешность положения точки определяют по формулам:
где
Общую редукцию (смещение точки Р в проектное положение Р0 и ее ориентировку) определяют по разности абсцисс и ординат указанных точек. В связи с большим объемом вычислений при малых величинах смещений, целесообразно пользоваться дифференциальным методом. Контроль определения осуществляется по четвертому опорному пункту. Необходимо помнить, что обратная засечка не имеет решения, если определяемая точка и все опорные точки находятся на проведенной через них окружности («опасная окружность»). По исследованиям, уход наружу и вовнутрь «опасной окружности» на расстояние 10% ее радиуса уже обеспечивает уверенное определение точки, так как сумма углов (j2 + b1 + b3)№180°.
|
- расстояния от опорных пунктов;
- дирекционные углы направлений засечки;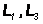
- расстояния между опорными пунктами 1 и 2, 2 и В;
- угол на пункте В между сторонами опорной сети.
