Адиабатное течение газов в каналах.
Рассмотрим случай, когда поток движется в канале переменного сечения без совершения техн. работы. Если геометрическая высота входа и выхода не меняется и течение адиабатно, то первый закон запишется:
Полученное соотношение показывает, что изменение скорости потока в канале всегда обратно по знаку изменению давления, т. е. если давление рабочего тела в канале уменьшается, то скорость его увеличивается, и наоборот. При этом условии понижение давления рабочего тела неизменно сопровождается расширением его, а повышение давления – сжатием. Каналы переменного сечения, в которых происходит расширение рабочего тела и скорость рабочего тела увеличивается, называются соплами. Они широко применяются в конструкциях паровых и газовых турбин и реактивных двигателях. Они используются для получения высокоскоростных газовых и паровых струй ударного действия (обдувочные аппараты). Каналы, в которых происходит обратный процесс и за счет уменьшения кинетической энергии потока производится сжатие рабочего тела, и давление повышается наз. диффузорами. Они широко применяются в технике, например в насосах, вентиляторах, струйных аппаратах и других нагнетателях, а также являются существенным элементом конструкции реактивных двигателей. Основой для вывода общих закономерностей движения рабочего тела в соплах и диффузорах является уравнение неразрывности потока: Полученное уравнение является уравнением неразрывности потока в дифференциальной форме. Преобразуем его для случая, когда раб. телом является идеальный газ. Логарифмируя уравнение адиабаты, получаем: Известно, что скорость распространения звука в газовой среде выражается формулой:
Наглядной характеристикой" состояния потока в любом сечении канала является отношение его скорости в данном сечении ω к местной скорости звука а. Это отношение называется числом Маха и обозначается буквой М,кг/сек. Значения М<1 соответствуют движению потока с дозвуковыми скоростями, а значения М>1 – со сверхзвуковыми скоростями. Используя число Маха уравнение неразрывности запишется: Данное выражение устанавливает зависимость изменения давления от геометрической формы канала и показывает, что при дозвуковых скоростях (М<.1) для понижения давления (dp<0) канал должен суживаться, а для повышения его – расширяться; при движении потока со сверхзвуковыми скоростями (М>l) картина получается обратной: чтобы давление понижалось, канал должен расширяться, для повышения давления – наоборот, суживаться. Рассмотренное показывает, что изменение давления и скорости потока создается противоположным воздействием геометрической формы канала на поток в зависимости от того, происходит ли движение его в дозвуковой или сверхзвуковой области. Это положение носит название закона геометрического обращения воздействия.
|

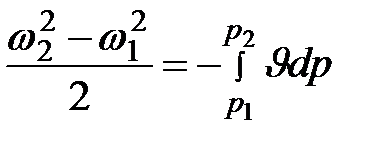 ,или в дифференциальной форме
,или в дифференциальной форме  .
. , где М – массовый расход рабочего тела; f – площадь произвольного сечения канала. Это уравнение показывает, что при стационарном режиме движения потока расход газа во всех сечениях канала одинаков. Логарифмируя его, получаем:
, где М – массовый расход рабочего тела; f – площадь произвольного сечения канала. Это уравнение показывает, что при стационарном режиме движения потока расход газа во всех сечениях канала одинаков. Логарифмируя его, получаем:  , а после дифференцирования:
, а после дифференцирования:  .
. , а после дифференцирования:
, а после дифференцирования:  , откуда
, откуда  . Поделим на ω2 уравнение, получим:
. Поделим на ω2 уравнение, получим:  . Подставляя полученное выражение в уравнение неразрывности в дифференциальной форме и получим:
. Подставляя полученное выражение в уравнение неразрывности в дифференциальной форме и получим:  , или
, или  .
.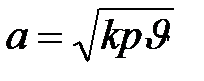 , к- показатель адиабаты. Следовательно,
, к- показатель адиабаты. Следовательно,  .
. .
.


