Задание 7. Вычислить неопределенный и определённый интегралы

Вычислить неопределенный и определённый интегралы.

 

№ вар.	неопределенный интеграл	определённый интеграл
	,
	,
	,
	,
	,
	,
	,
	,
	,
	,

 

 

 

 

Задание 8

Решить задачи, соответствующие варианту

 

Вариант 1.

 

Случайная величина X характеризуется рядом распределения:

Х
Р	0,4	0,2	0,1	0,3

Найти математическое ожидание и дисперсию случайной величины.

 

 

Вариант 2.

 

Найти дисперсию и среднее квадратическое отклонение дискретной случайной величины Х, заданной законом распределения:

Х	-5
Р	0,4	0,3	0,1	0,2

 

Вариант3.

 

Случайная величина X характеризуется рядом распределения:

Х
Р	0,2	0,4	0,3	0,08	0,02

Определить математическое ожидание и дисперсию случайной величины

Вариант4.

 

Случайная величина X задана функцией распределения

Найти вероятность того, что в результате испытания величина Х примет значение, заключенное в интервале (0;1/3).

 

 

Вариант5.

 

Случайная величина Xзадана функцией распределения

Найти вероятность того, что в результате испытания Х примет значение, заключенное в интервале (2;3).

 

Вариант6.

 

Найти математическое ожидание случайной величины Х, заданной функцией распределения

 

Вариант7.

Найти дисперсию случайной величины Х, заданной функцией распределения

Вариант8.

Случайная величина X распределена по нормальному закону с математическим ожиданием 40 и дисперсией 200. Вычислить вероятность попадания случайной величины в интервал (30, 80).

 

 

Вариант9.

Математическое ожидание и среднее квадратическое отклонение нормально распределенной случайной величины Х соответственно равны 10 и 2. Найти вероятность того, что в результате испытания Х примет значение, заключенное в интервале (12, 14).

 

Вариант10.

Случайная величина X характеризуется рядом распределения:

Х	-2	-1
Р	0,1	0,2	0,3	0,3	0,1

Определить математическое ожидание и дисперсию случайной величины

 

Рекомендуемая литература:

1. Конспект лекций по высшей математике. Часть 1 / Д. Т. Письменный. – 5-е изд. – М.: Айрис-пресс, 2005. – 208 с.: ил.

2. Конспект лекций по высшей математике. Часть 2 / Д. Т. Письменный. – 5-е изд. – М.: Рольф, 2000. – 256 с.: ил.

3. Сборник задач по высшей математике. 1 курс / К. Н. Лунгу, Д. Т. Письменный, С. Н. Федин, Ю. А. Шевченко. – 7-е изд. – М.: Айрис-пресс, 2008. – 576 с.: ил. – (Высшее образование).

4. Сборник задач по высшей математике. 2 курс / К. Н. Лунгу и др.; под ред. С. Н. Фенина. – 6-е изд. – М.: Айрис-пресс, 2007. – 592 с.: ил. ­ (Высшее образование).

5. Теория вероятностей и математическая статистика: учеб. пособие для вузов / В. Е. Гмурман. 9-е изд. ­­– М.: высш. шк., 2003. – 479 с.

6. Руководство к решению задач по теории вероятностей и математической статистике: учеб. пособие для студентов вузов / В. Е. Гмурман. 9-е изд. ­­– М.: высш. шк., 2004. – 404 с.

7. Баврин, И. И. Высшая математика: учебник / И. И. Баврин. - 3-е изд., стер. - М.: Академия, 2003. - 612 с.

8. Данко П. Е. Высшая математика в упражнениях и задачах. В 2 ч. - Б. Г. Данко П. Е. Ч. 1 [Текст] / П. Е. Данко, А. Г. Попов, Т. Я. Кожевникова. - 6-е изд. - М.: Мир и образование, 2003. - 304 с.

9. Данко П. Е. Высшая математика в упражнениях и задачах. В 2 ч. - Б. Г. Данко П. Е. Ч.2 [Текст] / П. Е. Данко, А. Г. Попов, Т. Я. Кожевникова. - 6-е изд. - М.: Мир и образование, 2003. - 416 с.

Уральский государственный университет физической культуры

Башкирский институт физической культуры

Кафедра «Гуманитарных и естественно-научных дисциплин»
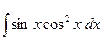
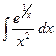