Заменив в (7.13) в соответствии с законом Ома , получим формулу
Соотношение (7.15) было установлено экспериментально в 1841 г. английским физиком Д. Джоулем и независимо от него в 1842 г. русским ученым Э. Х. Ленцем и носит название закона Джоуля–Ленца: количество теплоты, выделяющейся в единицу времени на участке цепи, при протекании по нему постоянного тока, равно произведению сопротивления участка цепи на квадрат силы тока.
Поскольку величины, фигурирующие в формуле (7.15), являются интегральными (характеризующими проводник конечных размеров), то можно сказать, что выражение (7.15) описывает закон Джоуля–Ленца в интегральной форме. От формулы (7.15), определяющей теплоту, выделяющуюся во всем проводнике, можно перейти к выражению, характеризующему выделение теплоты в различных местах проводника. Выделим в проводнике таким же образом, как это было сделано при выводе формулы (7.9), элементарный объем в виде цилиндра (см. рис. 7.1). Согласно закону Джоуля–Ленца за время
где Разделив выражение (7.16) на
Используя дифференциальную форму закона Ома [формула (7.9)] и соотношение
Формула (7.18) представляет собой дифференциальную форму закона Джоуля–Ленца. Отметим, что Джоуль и Ленц установили свой закон для однородного участка цепи. Однако, как следует из выкладок, приведенных в данном параграфе, формулы (7.15) и (7.18) справедливы и для неоднородного участка при условии, что действующие в нем сторонние силы имеют нехимическое происхождение. § 5. Разветвленные цепи. Правила Кирхгофа
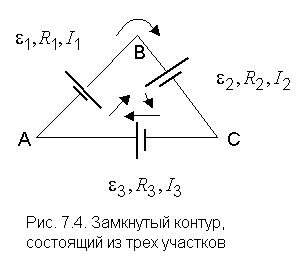
Например (рис. 7.3), первое правило Кирхгофа запишется так:
Первое правило вытекает из закона сохранения электрического заряда. В случае установившегося постоянного тока ни в одной точке проводника не должны накапливаться электрические заряды. В противном случае токи не могли бы оставаться постоянными. Уравнение (7.19) можно написать для каждого из N узлов цепи. Однако независимыми являются только N – 1 уравнений, N-e будет следствием из них.
При сложении этих выражений потенциалы взаимно уничтожаются и получается уравнение
которое выражает второе правило Кирхгофа: в любом замкнутом контуре, произвольно выбранном в разветвленной цепи, алгебраическая сумма произведений сил токов
Уравнение (7.20) может быть составлено для всех замкнутых контуров, которые можно выделить мысленно в данной разветвленной цепи. Однако независимыми будут только уравнения для тех контуров, которые нельзя получить наложением других контуров один на другой. При составлении уравнений второго правила Кирхгофа токам и эдс нужно приписывать знаки в соответствии с выбранным направлением обхода. Эдс также нужно приписать знак минус, так как она действует в направлении, противоположном направлению обхода. Направления обхода в каждом из контуров можно выбирать совершенно произвольно и независимо от выбора направлений в других контурах. При этом может случиться, что один и тот же ток либо одна и та же эдс войдет в разные уравнения с различными знаками. Это, однако, не имеет никакого значения, потому что изменение направления обхода вызывает лишь изменение всех знаков в уравнении (7.20) на обратные. Число независимых уравнений, составленных в соответствии с первым и вторым правилами Кирхгофа, оказывается равным числу различных токов, текущих в разветвленной цепи. Поэтому, если заданы эдс и сопротивления для всех неразветвленных участков, то могут быть вычислены все токи.
|
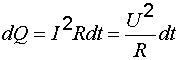. (7.15)
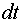в этом объеме выделится теплота
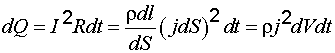, (7.16)
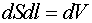– элементарный объем.
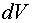и 
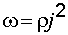. (7.17)
, получим 
. (7.18)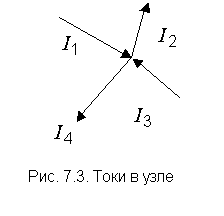 
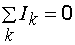.(7.19)
.
,
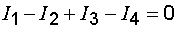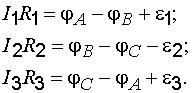
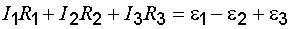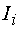на сопротивления 
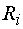соответствующих участков этого контура равна алгебраической сумме эдс 
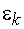, встречающихся в этом контуре: 
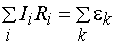. (7.20)
