РАСПРЕДЕЛЕННЫЙ АЛГОРИТМ БЕЛЛМАНА-ФОРДА
Будем считать, что длина dij, каждого ребра графа сети положительна. В принципе длина dij, может изменяться во времени, но примем, что все изменения в сети произошли до момента t0 и остаются фиксированными после него, по крайней мере, до построения кратчайшего маршрута.
Исходный граф сети А)
P={1,2} P={1,2,5}
г)д)
P={1,2,5,3,4} P={1,2,5,3,4,6} Рис. 2.2.
Пусть известно Di кратчайшее расстояние от каждого узла до узла-получателя информации, которым для конкретности будем считать узел 1. Можно показать, что: Di=min [dij+Dj], " i¹1, D1=0. (2.1) jÎN(i) Здесь N(i) - множество соседей узла i, т.е. узлов, соединенных с узлом i линией связи. Асинхронный вариант распределенного алгоритма Беллмана-Форда работает нерегламентированно время от времени (например, при изменении dij или Dj), выполняя операцию (2.1) в каждом узле i¹1 передавая измененное значение Di соседям. В результате каждый узел будет знать не только свое кратчайшее расстояние Di, но и уходящую от него линию, лежащую на кратчайшем пути к узлу 1. Особенностью данного алгоритма является то, что для его работы в узлах сети необходимо хранить очень мало информации и не нужны подробные сведения о топология всей сети - вполне достаточно знать длины уходящих от узла линий и обмениваться о соседями информацией о кратчайших расстояниях Di на данный момент. Именно на данном алгоритме маршрутизации был основан первоначальный алгоритм сети ARPANET, он также близок к алгоритму используемого в сети DNA фирмы DEC. Совокупность значений Di, образует "рельеф" сети, поэтому рассматриваемый метод является разновидностью метода рельефов.
|



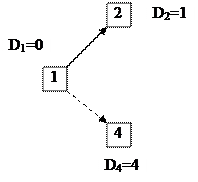
 б)в)
б)в)



