Определение напряженности поля в произвольной точкеЧерез точку, заданную преподавателем, проведем часть силовой линии вектора Е. Это дуга, проходящая через заданную точку между найденными эквипотенциальными поверхностями, между которыми оказалась заданная точка. Начинается дуга на одной из эквипотенциальных поверхностей, а заканчивается на другой поверхности, причем в начале и в конце эта дуга перпендикулярна эквипотенциальным поверхностям. Расстояние между поверхностями (длину дуги) обозначим через Для приближенного определения модуля вектора напряженности электрического поля воспользуемся декартовой системой координат с началом в рассматриваемой точке. В декартовой системе координат с началом в рассматриваемой точке и осью z, направленной перпендикулярно эквипотенциальной поверхности, проходящей через эту точку, формула связи E = -grad j между напряженностью поля и потенциалом запишется в виде
Изменяя мысленно расстояние между эквипотенциальными поверхностями, получим приближенную формулу для определения модуля напряженности электрического поля в рассматриваемой точке
Здесь
|
n. Искомый вектор Е в заданной точке направлен по касательной к изображенной части силовой линии в сторону убывания потенциала.
.
= 
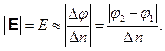
