Как линейная оптимизационная модель
Вариант – 1 Выполнили: Студенты группы ДПМ-81 Барсуков Р. В. Глебова О. В. Логинов С.
Проверил: Попович В. С.
Барнаул
Транспортная модель соответствует типовой задаче строительной индустрии: товарный продукт от m бетоносмесительных заводов определенной производительности нужно перевозить к n строительным объектам; для каждого объекта требуется определенное количество продукта; расстояние между заводами и объектами известно; необходимо определить, сколько бетона с каждого завода и на какой объект надо перевезти, чтобы грузоперевозки (тонно-километры и т. п.) были минимальными. Вводятся обозначения: i — заводы Задача, транспортного типа, оптимизации плана перевозок, формулируется как минимизация грузооборота.
Таблица 1 – Расстояния между заводами и потребителями бетона
Мощность бетоносмесительных заводов: 50, 15, 100 (м3). Потребности строительных объектов: 65, 45, 30, 25 (м3/ч). Поскольку суммарный объем производства товарного бетона (50 + 15 + 100) м /ч больше суммарного спроса (65 + 45 + 30 + 25) м3/ч, данная задача является замкнутой. Целевая функция:
при условиях:
Модель задачи содержит избыточное ограничение (2): если любые m+n–1 ограничений задачи удовлетворяются, то автоматически удовлетворяется и оставшееся ограничение. Таким образом, любое из уравнений спроса и поставок можно опустить. Следовательно, транспортная модель содержит m + n–1 независимых ограничений, вследствие чего в любое допустимое базисное решение входит также m +n – 1 базисных переменных. Исходную модель и процесс численного решения транспортной задачи можно представить в компактном виде при помощи транспортной таблицы (таблицы 2). Она имеет вид матрицы, i -я строка которой соответствует i -му пункту производства, а j -й столбец — j -му пункту спроса; ij -й элемент матрицы представляется прямоугольным «окошком», которое называется ячейкой таблицы. Расстояния между заводами и объектами рij даются в правом верхнем углу ij -ячейки. Левый верхний угол заполняется оценками оптимальности dij, смысл и назначение которых поясняются ниже. Наконец, в большом треугольнике в центре ячейки находится значение искомого объема перевозок — переменной Хij (если оно нулевое, то его можно опустить).
Таблица 2 - Общий вид транспортной таблицы
|

 1 Исходные данные
1 Исходные данные ; j — строящиеся объекты
; j — строящиеся объекты  ; ai — количество продукта, производимое i -м заводом, т; bj — потребность в продукте j -ro объекта, т; рij — расстояние от i -ro завода до j -ro объекта строительства, км; Хij — количество бетона, перевозимое с i -ro завода на j -и объект, т.
; ai — количество продукта, производимое i -м заводом, т; bj — потребность в продукте j -ro объекта, т; рij — расстояние от i -ro завода до j -ro объекта строительства, км; Хij — количество бетона, перевозимое с i -ro завода на j -и объект, т.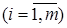
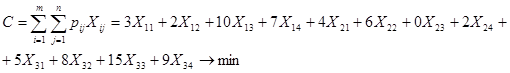 (1)
(1) или50+15+100 = 65 + 45+30 + 25; (2)
или50+15+100 = 65 + 45+30 + 25; (2)
 (3)
(3)
 d11 p11
x11
d11 p11
x11

 d12 p12
x12
d12 p12
x12
 Численное решение задачи, или определение оптимального плана перевозок, согласно сформулированному выше критерию оптимальности можно производить симплекс-методом.Однако такие особенности транспортной модели, как избыточность ограничений и равенство единице всех коэффициентов в уравнениях-ограничениях (3), позволяют упростить процедуры поиска включаемой в базис и выводимой из него переменных. При этом вместо проверки условия оптимальности по симплекс-критерию I (минимизация целевой функции) используется определение потенциалов, а построение замкнутого цикла заменяет процедуру применения симплекс-критерия II (условия допустимости). Для этого варианта симплекс-метода иногда используется название «метод потенциалов».
Численное решение задачи, или определение оптимального плана перевозок, согласно сформулированному выше критерию оптимальности можно производить симплекс-методом.Однако такие особенности транспортной модели, как избыточность ограничений и равенство единице всех коэффициентов в уравнениях-ограничениях (3), позволяют упростить процедуры поиска включаемой в базис и выводимой из него переменных. При этом вместо проверки условия оптимальности по симплекс-критерию I (минимизация целевой функции) используется определение потенциалов, а построение замкнутого цикла заменяет процедуру применения симплекс-критерия II (условия допустимости). Для этого варианта симплекс-метода иногда используется название «метод потенциалов».


