Определение вводимой в базис переменной
Определение вводимой в базис переменной основывается на критерии оптимальности симплекс-метода, модифицированном применительно к решению транспортной задачи. В методе потенциалов строке i и столбцу j транспортной таблицы (таблица 2) ставятся в соответствие некоторые числа, называемые потенциалами ui и vj. Для каждой базисной переменной Хij текущего решения сумма потенциалов должна быть равна соответствующему коэффициенту целевой функции:
Уравнения (4), число которых соответствует числу базисных переменных (m + n — 1), составляют систему, в которой (m + n) неизвестных. Значения потенциалов ui и vj определяются из этой системы, если придать одному из неизвестных (удобно наиболее часто встречающемуся) произвольное значение, например равное нулю. После этого для каждой небазисной Xpq переменной определяются оценки (критерии) оптимальности:
В базис включается та переменная Xpq, которая имеет наибольшую положительную оценку оптимальности. Если среди оценок dpq нет положительных, то данный опорный план — оптимальный. Уравнения, связанные с базисными переменными, имеют вид:
Пусть u1= 0. Тогда значения потенциалов: v1= 3, u2=1, v2=5, u3= 3,v3=12, v4= 6. Оценки dqp для небазисных переменных:
Наибольшую положительную оценку имеет Простая структура уравнений
Таблица 5 – Потенциалы ui и vj и оценки оптимальности первой операции, полученной по упрощенной схеме
Требуется найти значения потенциалов ui и vj, первой итерации решения задачи, пользуясь упрощенной схемой. Согласно таблице 4, выбирается u3 = 0. Справа от 3-й строки можно проставить значение u3. Строка (столбец), соответствующая u3, просматривается для выявления базисных переменных. В строке 3 базису принадлежат x32, x33, x34. С помощью уравнения (4) находятся значения потенциалов: v2 = p32 –u3 = 8, v3 = p33 – u3 = = 15-0 =15, v4= p34-u3 = 9-0 = 9. Вычисление остальных потенциалов проводится по вышеизложенной схеме (u2=-2, u1=-3, v1 = 6) и заносится в таблицу 5. Теперь можно вычислить оценки dpq для небазисных xpq и занести их в соответствующие ячейки. Как видно из таблицы 5, значения потенциалов ui и vj, а также оценки dpq отличаются от значений, полученных при непосредственном решении системы уравнений (4), (5). Это вызвано выбором в качестве свободного потенциала переменной u2 вместо u1. Однако по критерию оптимальности наибольшее положительное значение dpq по-прежнему имеет небазисная переменная х23 которая и включается в базис.
|

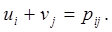 (4)
(4)
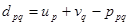 (5)
(5)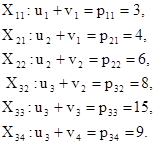
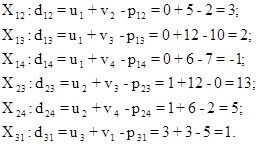
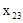 , которую следует включить в базис.
, которую следует включить в базис.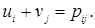 позволяет, не записывая систему уравнений, находить потенциалы непосредственно по транспортной таблице. Вначале в левых верхних углах ячеек, соответствующих каждой базисной переменной хij на текущей итерации, проставляются символы 0. Выбирается любая величина — uiили vj. Ей присваивается произвольное значение, проставляемое у строки или столбца, которым принадлежит выбранное uiили vj. Строка или столбец анализируется с целью выявления базисных переменных данной итерации. Если выбрана строка i и базисные переменные в ней хil, xir и xis, то уравнение (4) позволяет найти значения потенциалов
позволяет, не записывая систему уравнений, находить потенциалы непосредственно по транспортной таблице. Вначале в левых верхних углах ячеек, соответствующих каждой базисной переменной хij на текущей итерации, проставляются символы 0. Выбирается любая величина — uiили vj. Ей присваивается произвольное значение, проставляемое у строки или столбца, которым принадлежит выбранное uiили vj. Строка или столбец анализируется с целью выявления базисных переменных данной итерации. Если выбрана строка i и базисные переменные в ней хil, xir и xis, то уравнение (4) позволяет найти значения потенциалов 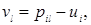

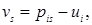 соответствующие столбцам, на пересечении которых с i-й строкой находятся базисные переменные. Полученные значения vi используются по аналогии для вычисления оставшихся потенциалов.
соответствующие столбцам, на пересечении которых с i-й строкой находятся базисные переменные. Полученные значения vi используются по аналогии для вычисления оставшихся потенциалов. После этого можно вычислить по (5) оценки оптимальности dpq для всех небазисных переменных xpq и проставить их в соответствующих левых углах ячеек таблицы 5.
После этого можно вычислить по (5) оценки оптимальности dpq для всех небазисных переменных xpq и проставить их в соответствующих левых углах ячеек таблицы 5. 1
1







 Ø 4
Ø 4

 Ø 6
Ø 6

 1 5
1 5

 Ø 8
Ø 8

 Ø 15
Ø 15

 Ø 9
Ø 9



