Показатели прочности грунта
Современные методы проектирования оснований и фундаментов по группам предельных состояний требуют достоверной оценки показателей прочности грунта – удельного сцепления с и угла внутреннего трения φ. Под действием внешних сил грунт в основании сооружениях сооружений находится в напряженном состоянии. Если мысленно выделить из массива элементарный объем грунта, то в общем случае он будет испытывать действие нормальных и касательных напряжений. В процессе увеличения нагрузки изменяется их величина и соотношение, происходит деформирование грунта, который на определенном этапе разрушается. Прочность пылевато-глинистых грунтов определяется активностью и числом связей между частицами. На ранней стадии формировании грунта его прочность обусловлена действием межмолекулярных сил, называемых силами Ван-дер-Ваальса, которое проявляется в виде сцепления. Это сцепление, названное первичным, зависит от плотности осадка, слагающего грунт. В результате соединения частиц в агрегаты и их цементации происходит вторичное сцепление упрочения, что способствует «консервации» неуплотненного состояния лессового грунта. Таким образом, прочность пылевато-глинистых грунтов обусловлена влиянием первичного сцепления и сцепления вторичного уплотнения, а также сил внутреннего трения. Показателем прочности грунтов является их сопротивление сдвигу, зависящее от физических свойств и напряженного состояния в образце или основании. Установлено, что в момент перехода от равновесия грунта к его разрушению существует зависимость между сопротивлением сдвигу τ и нормальным давлением р, приложенным к плоскости сдвига, следующего вида
Доказано, что природа сил сопротивления сдвигу имеет сложный характер. Уравнение (2.14) можно рассматривать как математическое выражение зависимости между τ и р, а величины с и φ, являющиеся параметрами уравнения, могут быть приняты как количественные характеристики прочности грунта. Многочисленные опыты свидетельствуют о том, что при замачивании лессовых грунтов, в отличии от обычных пылевато-глинистых грунтов, наблюдается существенное уменьшение их удельного сцепления и небольшое снижение силы трения. Как отмечалось ранее в расчетах оснований, должны использоваться физико-механические характеристики лессовых грунтов, соответствующих определенному значению прогнозируемой влажности. Показатели прочности лессовых грунтов с и φ в инженерной практике определяются в условиях лабораторных испытаний на сдвиг. Определение показателей прочности грунта естественной влажности и в водонасыщенном состоянии обычно не представляется затруднительным. Более сложным является установление прочности при промежуточном значении влажности. В лабораторных условиях она может быть достигнута введением в образец строго дозированного количества воды. Однако для массовых определений прочности грунта на сдвиг такой метод оказывается трудоемким. В результате статистической обработки большого количества сдвиговых опытов установлено, что зависимость показателей прочности сw и φw при промежуточном значении влажности w лессовых грунтов может быть выражена через сn и сsat, φn и φsat, соответствующих естественной влажности и водонасыщенному состоянию грунта. Формулы имеют следующий вид:
В отдельных случаях при отсутствии данных непосредственных определений с и φ, нормативные документы допускают использование региональных таблиц, содержащих их нормативные значения (табл. 1).
|

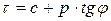 . (2.14)
. (2.14)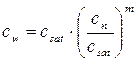 ; (2.15)
; (2.15)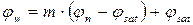 ; (2.16)
; (2.16)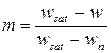 . (2.17)
. (2.17)


