Задание 12.
12.1. Случайная величина 12.2. Случайная величина 12.3. Случайная величина 12.4. Случайная величина 12.5. Случайная величина 12.6. Случайная величина 12.7. Случайная величина 12.8. Случайная величина 12.9. Случайная величина 12.10. Случайная величина 12.11. Случайная величина 12.12. Случайная величина 12.13. Случайная величина 12.14. Случайная величина 12.15. Случайная величина 12.16. Случайная величина 12.17. Случайная величина 12.18. Случайная величина 12.19. Случайная величина 12.20. Случайная величина 12.21. Случайная величина 12.22. Случайная величина 12.23. Случайная величина 12.24. Случайная величина 12.25. Случайная величина 12.26. Случайная величина 12.27. Случайная величина 12.28. Случайная величина 12.29. Случайная величина 12.30. Случайная величина
Задание 13. Законы распределения. Нормальное распределение.
13.1. Автомат изготавливает подшипники, которые считаются годными, если отклонение 13.2. Пачки печенья упаковывают автоматически. Масса пачки распределена по нормальному закону и имеет среднее значение 200 г, среднеквадратичное отклонение 5 г. Найти вероятность того, что вес случайно взятой пачки меньше 195 г. 13.3. Детали, выпускаемые цехом, исходя из диаметра распределяются по нормальному закону с такими параметрами: математическое ожидание равно 5 см; дисперсия равна 0,81. Найти вероятность того, что диаметр наудачу взятой детали отличается от математического ожидания не более чем на 2 см. 13.4. При взвешивании получается ошибка, подчиненная нормальному закону с 13.5. Детали, выпускаемые цехом, исходя из диаметра распределяются по нормальному закону с такими параметрами: математическое ожидание равно 5 см, а дисперсия равна 0,81. Найти границы, в которых следует ожидать размер диаметра детали, чтобы вероятность невыхода за эти границы была равна 0,95. 13.6. Результаты измерения расстояния между двумя населенными пунктами подчинены нормальному закону с параметрами: математическое ожидание равно 16 км, а среднее квадратичное отклонение равно 100 м. Найти вероятность того, что расстояние между этими пунктами не меньше 15,8 км. 13.7. Рост взрослых женщин является случайной величиной, распределенной по нормальному закону. Математическое ожидание ее пусть равно 164 см, а среднее квадратичное отклонение 5,5 см. Найти плотность вероятности и функцию распределения этой случайной величины. Вычислить вероятность того, что ни одна из пяти наудачу выбранных женщин не будет иметь рост более 160 см. 13.8. Результаты измерения расстояния между двумя населенными пунктами подчинены нормальному закону с такими параметрами: математическое ожидание равно 20 км; среднеквадратичное отклонение равно 100 м. Найти вероятность того, что расстояние между этими пунктами не менее 17-ти км, но не более 21-го км. 13.9. Отклонение длины изготавливаемых деталей от стандарта есть случайная величина, распределенная по нормальному закону. Стандартная длина равна 20 сантиметров, среднее квадратичное отклонение равно 0,1 см. Определить, какую точность изделия можно гарантировать с вероятностью 0,9. 13.10. Результаты измерения расстояния между двумя населенными пунктами подчинены нормальному закону с такими параметрами: математическое ожидание равно 20 км; среднеквадратичное отклонение равно 100 м. Найти вероятность того, что расстояние между этими пунктами не более 21 км. 13.11. Детали, выпускаемые цехом, исходя из размера диаметра распределяются по нормальному закону с такими параметрами: математическое ожидание равно 7 см; дисперсия равна 0,7. Установить границы, в которых следует ожидать размер диаметра детали, чтобы вероятность невыхода за эти границы была равна 0,95. 13.12. Диаметр деталей, изготовленных цехом, является случайной величиной, распределенной по нормальному закону. Математическое ожидание равно 2,5 см, а дисперсия – 0,0001. В каких границах можно практически гарантировать диаметр детали (за достоверное принимается событие, вероятность которого равна 0,9973)? 13.13.Результаты измерения расстояния между двумя населенными пунктами подчинены нормальному закону с такими параметрами: математическое ожидание равно 16 км; а среднеквадратичное отклонение равно 100 м. Найти вероятность того, что расстояние между этими пунктами не меньше 15,8 км. 13.14.Автомат изготавливает шарики. Шарик считается годным, если отклонение 13.15. Детали, выпускаемые цехом, исходя из диаметра распределяются по нормальному закону с такими параметрами: математическое ожидание равно 7 см; дисперсия равна 0,7. Найти вероятность того, что диаметр наудачу взятой детали — от 3 до 5 см. 13.16. Поезд состоит из 100 вагонов. Масса каждого вагона - случайная величина, распределенная по нормальному закону с математическим ожиданием 13.17. Детали, выпускаемые цехом, исходя из размера диаметра распределяются по нормальному закону с такими параметрами: математическое ожидание равно 7 см; дисперсия равна 0,7. Найти вероятность того, что диаметр наудачу взятой детали отличается от математического ожидания не более чем на 2 см. 13.18. При измерении детали получаются случайные ошибки, подчиненные нормальному закону с 13.19. Результаты измерения расстояния между двумя населенными пунктами подчинены нормальному закону со следующими параметрами: математическое ожидание равно 16 км, а среднеквадратичное отклонение равно 100 м. Найти вероятность того, что расстояние между этими пунктами не менее 15,75 км, но не более 16,3 км. 13.20. Рост взрослых мужчин является случайной величиной, распределенной по нормальному закону. Пусть ее математическое ожидание равно 178 см, а дисперсия – 32. Найти плотность вероятности и функцию распределения этой случайной величины. Вычислить вероятность того, что хотя бы один из наудачу выбранных пяти мужчин будет иметь рост от 168 до 182 см. 13.21.При взвешивании получается ошибка, подчиненная нормальному закону с 13.22. Станок-автомат изготавливает валики, контролируя их диаметры 13.23. Результаты измерения расстояния между двумя населенными пунктами подчинены нормальному закону с такими параметрами: математическое ожидание равно 16 км, а среднеквадратичное отклонение равно 100 м. Найти вероятность того, что расстояние между этими пунктами не более 16,25 км. 13.24. При измерении детали получаются случайные ошибки, подчиненные нормальному закону с 13.25. Детали, выпускаемые цехом, исходя из диаметра распределяются по нормальному закону с такими параметрами: математическое ожидание равно 5 см; дисперсия равна 0,81. Найти вероятность того, что диаметр наудачу взятой детали – от 4 до 7 см. 13.26.Случайная величина 13.27. Результаты измерения расстояния между двумя населенными пунктами подчинены нормальному закону с такими параметрами: математическое ожидание равно 20 км; среднеквадратичное отклонение равно 100 м. Найти вероятность того, что расстояние между этими пунктами не меньше 18 км. 13.28. Рост взрослых мужчин является случайной величиной, распределенной по нормальному закону. Математическое ожидание ее пусть равно 170 см, а дисперсия – 36. Найти плотность вероятности и функцию распределения этой случайной величины. Вычислить вероятность того, что хотя бы один из наудачу выбранных четырех мужчин будет иметь рост от 168 до 172 см. 13.29. При взвешивании получается ошибка, подчиненная нормальному закону с 13.30.Считается, что отклонение длины изготавливаемых деталей от стандарта является случайной величиной, распределенной по нормальному закону. Если стандартная длина
Задание 14. Законы распределения
14.1. Случайная величина 14.2. Математическое ожидание нормально распределенной случайной величины 14.3. Математическое ожидание нормально распределенной случайной величины 14.4. Математическое ожидание нормально распределенной случайной величины 14.5. Для случайной величины 14.6. Случайная величина 14.7. Случайная величина 14.8. Математическое ожидание нормально распределенной случайной величины 14.9. Распределение веса деталей, выпускаемых заводом, подчиняется нормальному закону со средним весом 40 г и среднеквадратическим отклонением 1 г. Найти вероятность того, что отклонение веса детали от среднего веса по абсолютной величине не превысит 1,5 г. 14.10. Для случайной величины 14.11. Случайная величина 14.12. Математическое ожидание нормально распределенной случайной величины 14.13. Случайные ошибки измерения подчинены нормальному закону со среднеквадратическим отклонением 1 мм и математическим ожиданием 0. Найти вероятность того, что при очередном измерении ошибка превзойдет 1,28 мм. 14.14. Для полета самолета отведен коридор 100 м. Самолет должен лететь по его средней линии, однако из-за систематической ошибки в показаниях высотометра он летит на 20 м выше. Случайная ошибка в показаниях прибора имеет среднее квадратичное отклонение 75 м. Какова вероятность того, что самолет будет лететь внутри коридора? 14.15. По какому закону распределена случайная величина 14.16. Для случайной величины 14.17. Случайное отклонение размера детали от номинала при изготовлении ее на данном станке имеет нулевое математическое ожидание и среднее квадратичное отклонение, равное 3 мк. Найти вероятность того, что две детали окажутся стандартными, если для годной детали допустимо отклонение не более чем на 4 мк. 14.18. Изделие является изделием высшего качества, если отклонение его размеров от номинала не превышает 3,45 мм. Случайные отклонения размера изделия от номинала подчиняются нормальному закону распределения со средним квадратичным отклонением, равным 3 мм, а систематические отклонения отсутствуют. Определить среднее число изделий высшего сорта, если изготовляются 4 изделия. 14.19. При большом числе измерений установлено, что 75 % ошибок не превосходят по абсолютной величине 1,25 мм. Определить среднее квадратичное отклонение ошибок измерения, считая их нормально распределенными с нулевым математическим ожиданием. 14.20. Средняя квадратичная ошибка измерения дальности радиолокатором равна 25м, систематическая ошибка отсутствует. Определить вероятность того, что ошибка не превзойдет 20 м. 14.21. Для случайной величины 14.22. При средней длине детали 20 см найдено, что отклонения, превосходящие 0,5, встречаются в среднем 4 раза на 100 деталей. Считая, что длина детали распределена по нормальному закону, определите ее среднее квадратичное отклонение. 14.23. Случайная величина 14.24. Математическое ожидание нормально распределенной случайной величины 14.25. Математическое ожидание нормально распределенной случайной величины 14.26. Непрерывная случайная величина 14.27. Математическое ожидание нормально распределенной случайной величины 14.28. Случайная величина 14.29. Случайная величина 14.30. По какому закону распределена случайная величина
|

 задана функцией распределения
задана функцией распределения  Найти а) плотность распределения
Найти а) плотность распределения 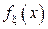 , б) дисперсию
, б) дисперсию  , в) вероятность
, в) вероятность 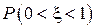 . Построить графики
. Построить графики  и
и 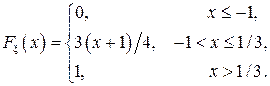 Найти а) плотность распределения
Найти а) плотность распределения  Найти а) плотность распределения
Найти а) плотность распределения 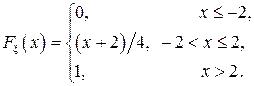 Найти а) плотность распределения
Найти а) плотность распределения 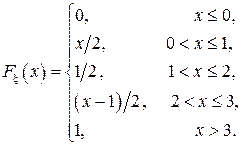 Найти: а) плотность распределения
Найти: а) плотность распределения 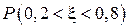 . Построить графики
. Построить графики  Найти: а) плотность распределения
Найти: а) плотность распределения 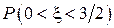 . Построить графики
. Построить графики  Найти: а) плотность распределения
Найти: а) плотность распределения 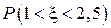 . Построить графики
. Построить графики 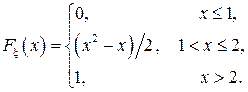 Найти: а) плотность распределения
Найти: а) плотность распределения 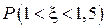 . Построить графики
. Построить графики  Найти: а) плотность распределения
Найти: а) плотность распределения  . Построить графики
. Построить графики 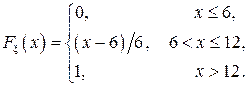 Найти: а) плотность распределения
Найти: а) плотность распределения  . Построить графики
. Построить графики 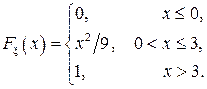 Найти: а) плотность распределения
Найти: а) плотность распределения  . Построить графики
. Построить графики  Найти: а) плотность распределения
Найти: а) плотность распределения  . Построить графики
. Построить графики  Найти: а) плотность распределения
Найти: а) плотность распределения  . Построить графики
. Построить графики 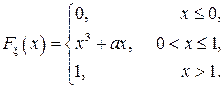 Найти: а) коэффициент
Найти: а) коэффициент  иплотность распределения
иплотность распределения  . Построить графики
. Построить графики  Найти: а) плотность распределения
Найти: а) плотность распределения  . Построить графики
. Построить графики  Найти: а) плотность распределения
Найти: а) плотность распределения  . Построить графики
. Построить графики  Найти: а) плотность распределения
Найти: а) плотность распределения  . Построить графики
. Построить графики 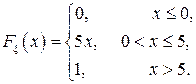 Найти: а) плотность распределения
Найти: а) плотность распределения  Найти: а) плотность распределения
Найти: а) плотность распределения 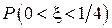 . Построить графики
. Построить графики  Найти: а) плотность распределения
Найти: а) плотность распределения 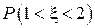 . Построить графики
. Построить графики  Найти: а) плотность распределения
Найти: а) плотность распределения  . Построить графики
. Построить графики  Найти: а) плотность распределения
Найти: а) плотность распределения  . Построить графики
. Построить графики  Найти: а) плотность распределения
Найти: а) плотность распределения  . Построить графики
. Построить графики 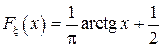 Найти: а) плотность распределения
Найти: а) плотность распределения  . Построить графики
. Построить графики 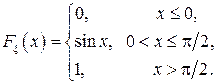 Найти: а) плотность распределения
Найти: а) плотность распределения 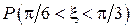 . Построить графики
. Построить графики 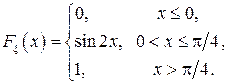 Найти: а) плотность распределения
Найти: а) плотность распределения  . Построить графики
. Построить графики 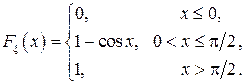 Найти: а) плотность распределения
Найти: а) плотность распределения 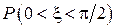 . Построить графики
. Построить графики 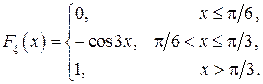 Найти: а) плотность распределения
Найти: а) плотность распределения 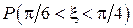 . Построить графики
. Построить графики  Найти: а) плотность распределения
Найти: а) плотность распределения  Найти: а) плотность распределения
Найти: а) плотность распределения 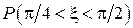 . Построить графики
. Построить графики  мм?
мм?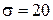 г. Найдите вероятность того, взвешивание будет произведено с ошибкой не превосходящей 40 г.
г. Найдите вероятность того, взвешивание будет произведено с ошибкой не превосходящей 40 г. диаметра шарика от проектного размера по абсолютной величине меньше 0,7 мм. Считая, что случайная величина
диаметра шарика от проектного размера по абсолютной величине меньше 0,7 мм. Считая, что случайная величина 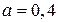 мм. Найти, сколько в среднем будет годных шариков из 100 изготовленных.
мм. Найти, сколько в среднем будет годных шариков из 100 изготовленных. т и средним квадратичным отклонением
т и средним квадратичным отклонением  т. Локомотив может везти состав массой не более 6600 т, в противном случае необходимо прицеплять второй локомотив. Найти вероятность того, что второй локомотив не потребуется.
т. Локомотив может везти состав массой не более 6600 т, в противном случае необходимо прицеплять второй локомотив. Найти вероятность того, что второй локомотив не потребуется. мм. Найдите вероятность того, что измерение будет произведено с ошибкой, не превосходящей 20 мм.
мм. Найдите вероятность того, что измерение будет произведено с ошибкой, не превосходящей 20 мм. мм,
мм, 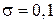 мм, найдите интервал, в котором с вероятностью 0,9973 будут заключены диаметры изготовленных валиков.
мм, найдите интервал, в котором с вероятностью 0,9973 будут заключены диаметры изготовленных валиков. . Найти интервал, симметричный относительно математического ожидания, в который с вероятностью
. Найти интервал, симметричный относительно математического ожидания, в который с вероятностью  попадет значение величины
попадет значение величины 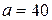 см и среднее квадратичное отклонение
см и среднее квадратичное отклонение 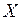 подчинена нормальному закону распределения с
подчинена нормальному закону распределения с 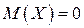 . Вероятность попадания ее значений в промежуток
. Вероятность попадания ее значений в промежуток  равна 0,25. Найти ее среднее квадратичное отклонение.
равна 0,25. Найти ее среднее квадратичное отклонение.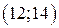 .
. .
.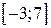 . Выписать плотность вероятности и функцию распределения, найти математическое ожидание
. Выписать плотность вероятности и функцию распределения, найти математическое ожидание  и дисперсию
и дисперсию 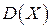 .
.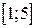 . Выписать плотность вероятности и функцию распределения, найти математическое ожидание
. Выписать плотность вероятности и функцию распределения, найти математическое ожидание  равна 0,3108. Найти дисперсию
равна 0,3108. Найти дисперсию  .
.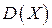 , функция распределения, если плотность вероятностей этой случайной величины есть
, функция распределения, если плотность вероятностей этой случайной величины есть 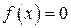 при
при 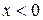 ,
,  при
при 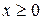 .
. . Выписать плотность вероятности и функцию распределения, найти математическое ожидание
. Выписать плотность вероятности и функцию распределения, найти математическое ожидание  , распределенной равномерно на отрезке
, распределенной равномерно на отрезке  . Выписать плотность вероятности и функцию распределения, найти математическое ожидание
. Выписать плотность вероятности и функцию распределения, найти математическое ожидание  и дисперсию
и дисперсию 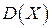 .
. подчинена нормальному закону распределения с
подчинена нормальному закону распределения с 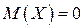 . Вероятность попадания ее значений в промежуток
. Вероятность попадания ее значений в промежуток  равна 0,45. Найти ее среднее квадратичное отклонение.
равна 0,45. Найти ее среднее квадратичное отклонение. .
. при
при  ,
,  при
при 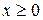 . Найти вероятность того, что в результате испытаний
. Найти вероятность того, что в результате испытаний  .
.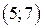 .
.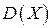 , функция распределения, если плотность вероятностей этой случайной величины есть
, функция распределения, если плотность вероятностей этой случайной величины есть  при
при 


