Индивидуальные задания №2
ВНМАНИЕ ВАЖНАЯ ИНФОРМАЦИЯ:
Каждому студенту необходимо выполнить 9 заданий, по одному заданию из каждой темы, под своим вариантом. Номер Вашего варианта соответствует Вашему номеру в журнале старосты. При этом:
Группы АСУ 13-01, АСУ 13-02, РТВ 13-03 начинают с первого варианта.
Группы РТВ 13-01, РТВ 13-02 начинают с 30 варианта в обратном порядке (т.е. 1 по списку делает 30 вариант, второй 29, и т.д.)
Если студент выполнил задания не соответствующие его варианту, то они учитываться не будут!
Задание 10. Дискретная случайная величина.
10.1. Стрелок производит по мишени три выстрела. Вероятность попадания в мишень при каждом выстреле равна 0,3. Построить ряд распределения случайной величины  – числа попаданий. Найти функцию распределения
– числа попаданий. Найти функцию распределения  , построить ее график, вычислить математическое ожидание
, построить ее график, вычислить математическое ожидание  и дисперсию
и дисперсию  .
.
10.2. В урне имеется 4 шара с номерами от 1 до 4. Вынули 2 шара. Случайная величина  – сумма номеров шаров. Построить ряд распределения случайной величины
– сумма номеров шаров. Построить ряд распределения случайной величины  . Найти функцию распределения
. Найти функцию распределения  , построить ее график, вычислить математическое ожидание
, построить ее график, вычислить математическое ожидание  и дисперсию
и дисперсию  .
.
10.3. В урне 6 белых и 4 черных шара. Из нее пять раз подряд извлекают шар, причем каждый раз вынутый шар возвращают в урну и шары перемешивают. Приняв за случайную величину  – число извлеченных белых шаров, составить закон распределения этой случайной величины. Найти функцию распределения
– число извлеченных белых шаров, составить закон распределения этой случайной величины. Найти функцию распределения  , построить ее график, вычислить математическое ожидание
, построить ее график, вычислить математическое ожидание  и дисперсию
и дисперсию  .
.
10.4. Из партии, состоящей из 100 изделий, среди которых имеется 10 бракованных, выбраны случайным образом пять изделий для проверки их качества. Построить ряд распределения случайного числа  бракованных изделий, содержащихся в выборке. Найти функцию распределения
бракованных изделий, содержащихся в выборке. Найти функцию распределения  , построить ее график, вычислить математическое ожидание
, построить ее график, вычислить математическое ожидание  и дисперсию
и дисперсию  .
.
10.5. На пути движения автомашины 4 светофора. Каждый из них с вероятностью 0,5 либо разрешает, либо запрещает автомашине дальнейшее движение. Построить ряд распределения случайной величины  – числа светофоров, пройденных автомашиной до первой остановки. Найти функцию распределения
– числа светофоров, пройденных автомашиной до первой остановки. Найти функцию распределения  , построить ее график, вычислить математическое ожидание
, построить ее график, вычислить математическое ожидание  и дисперсию
и дисперсию  .
.
10.6. Производятся последовательные испытания пяти приборов на надежность. Каждый следующий прибор испытывается только в том случае, если предыдущий оказался надежным. Построить ряд распределения случайной величины  – случайного числа испытанных приборов, если вероятность выдержать испытания для каждого из них равна 0,9. Найти функцию распределения
– случайного числа испытанных приборов, если вероятность выдержать испытания для каждого из них равна 0,9. Найти функцию распределения  , построить ее график, вычислить математическое ожидание
, построить ее график, вычислить математическое ожидание  и дисперсию
и дисперсию  .
.
10.7. Из урны, содержащей 6 белых и 4 черных шаров, случайным образом и без возвращения извлекается 3 шара. Случайная величина  – число белых шаров в выборке. Описать закон распределения. Найти функцию распределения
– число белых шаров в выборке. Описать закон распределения. Найти функцию распределения  , построить ее график, вычислить математическое ожидание
, построить ее график, вычислить математическое ожидание  и дисперсию
и дисперсию  .
.
10.8. Из 25 радиоламп, среди которых 10 бракованных, случайным образом выбраны 5 радиоламп для проверки их параметров. Определить и построить: 1) ряд распределения числа  бракованных радиоламп; 2) функцию распределения
бракованных радиоламп; 2) функцию распределения  ; 3) математическое ожидание
; 3) математическое ожидание  ; 4) дисперсию
; 4) дисперсию  .
.
10.9. Охотник стреляет по дичи до первого попадания, но успевает сделать не более четырех выстрелов. Составить закон распределения случайной величины  – числа выстрелов, производимых охотником. Вероятность попадания в цель при одном выстреле равна 0,7. Найти функцию распределения
– числа выстрелов, производимых охотником. Вероятность попадания в цель при одном выстреле равна 0,7. Найти функцию распределения  , построить ее график. Определить математическое ожидание
, построить ее график. Определить математическое ожидание  и дисперсию
и дисперсию  .
.
10.10. Стрелок производит по мишени 3 выстрела. Вероятность попадания в мишень при каждом выстреле равна 0,3. Построить ряд распределения случайной величины  – числа попаданий. Найти функцию распределения
– числа попаданий. Найти функцию распределения  , построить ее график. Определить математическое ожидание
, построить ее график. Определить математическое ожидание  и дисперсию
и дисперсию  .
.
10.11. Вероятность того, что в библиотеке необходимая студенту книга свободна, равна 0,3. Составить закон распределения случайной величины  – числа библиотек, которые посетит студент, если в городе четыре библиотеки. Найти функцию распределения
– числа библиотек, которые посетит студент, если в городе четыре библиотеки. Найти функцию распределения  , построить ее график. Определить математическое ожидание
, построить ее график. Определить математическое ожидание  и дисперсию
и дисперсию  .
.
10.12. Вероятность попадания в цель при одном выстреле из орудия равна 0,4. Производится 6 выстрелов. Составить закон распределения случайной величины  – числа попаданий. Найти функцию распределения
– числа попаданий. Найти функцию распределения  , построить ее график. Определить математическое ожидание
, построить ее график. Определить математическое ожидание  и дисперсию
и дисперсию  .
.
10.13. При установившемся технологическом процессе  всей продукции станок-автомат выпускает первым сортом, а
всей продукции станок-автомат выпускает первым сортом, а  – вторым. Построить ряд распределения случайной величины
– вторым. Построить ряд распределения случайной величины  и функцию распределения
и функцию распределения  числа изделий второго сорта среди 5 штук отобранных случайным образом. Построить график
числа изделий второго сорта среди 5 штук отобранных случайным образом. Построить график  . Определить математическое ожидание
. Определить математическое ожидание  и дисперсию
и дисперсию  .
.
10.14. По одной и той же стартовой позиции противника производится пуск 5 ракет, причем вероятность попадания в цель при каждом пуске равна 0,8. Построить ряд распределения случайной величины  – числа попадания, функцию распределения
– числа попадания, функцию распределения  . Построить график
. Построить график  . Определить математическое ожидание
. Определить математическое ожидание  и дисперсию
и дисперсию  .
.
10.15. Устройство состоит из 3-х независимо работающих элементов. Вероятность отказа каждого элемента в данном опыте равна 0,1. Составить ряд распределения случайной величины  – числа отказавших элементов в данном опыте. Найти функцию распределения
– числа отказавших элементов в данном опыте. Найти функцию распределения  , построить ее график, вычислить математическое ожидание
, построить ее график, вычислить математическое ожидание  и дисперсию
и дисперсию  .
.
10.16. Составить ряд распределения случайной величины  – числа появления “герба” при двух подбрасываний монеты. Найти функцию распределения
– числа появления “герба” при двух подбрасываний монеты. Найти функцию распределения  , построить ее график, вычислить математическое ожидание
, построить ее график, вычислить математическое ожидание  и дисперсию
и дисперсию  .
.
10.17. В партии 10 деталей, среди которых 3 нестандартных, наудачу отобраны 2 детали. Найти математическое ожидание и дисперсию случайной величины  – числа нестандартных деталей среди 2-х отобранных. Найти функцию распределения
– числа нестандартных деталей среди 2-х отобранных. Найти функцию распределения  , построить ее график, вычислить математическое ожидание
, построить ее график, вычислить математическое ожидание  и дисперсию
и дисперсию  .
.
10.18. Составить ряд распределения случайной величины  – числа появления события
– числа появления события  в 3-х независимых испытаниях, если вероятность появления события
в 3-х независимых испытаниях, если вероятность появления события  в каждом испытании равна
в каждом испытании равна  . Найти функцию распределения
. Найти функцию распределения  , построить ее график, вычислить математическое ожидание
, построить ее график, вычислить математическое ожидание  и дисперсию
и дисперсию  .
.
10.19. В городе 4 библиотеки. Вероятность того, что необходимая студенту книга свободна, равна  для каждой библиотеки. Составить ряд распределения случайной величины
для каждой библиотеки. Составить ряд распределения случайной величины  – числа библиотек, которые посетит студент. Найти функцию распределения
– числа библиотек, которые посетит студент. Найти функцию распределения  , построить ее график, вычислить математическое ожидание
, построить ее график, вычислить математическое ожидание  и дисперсию
и дисперсию  .
.
10.20. В партии из 6 деталей имеется 4 стандартных. Наудачу отобраны 3 детали. Составить ряд распределения случайной величины  – числа стандартных деталей среди 3-х отобранных. Найти функцию распределения
– числа стандартных деталей среди 3-х отобранных. Найти функцию распределения  , построить ее график, вычислить математическое ожидание
, построить ее график, вычислить математическое ожидание  и дисперсию
и дисперсию  .
.
10.21. Производится 4 выстрела по мишени. Вероятность попадания при каждом выстреле –  . Составить ряд распределения случайной величины
. Составить ряд распределения случайной величины  – числа попаданий. Найти функцию распределения
– числа попаданий. Найти функцию распределения  , построить ее график, вычислить математическое ожидание
, построить ее график, вычислить математическое ожидание  и дисперсию
и дисперсию  .
.
10.22. Из 10 радиоламп, среди которых 3 бракованных, случайным образом выбраны 4 радиолампы для проверки их параметров. Составить ряд распределения случайной величины  – числа бракованных радиоламп в выборке. Найти функцию распределения
– числа бракованных радиоламп в выборке. Найти функцию распределения  , построить ее график, вычислить математическое ожидание
, построить ее график, вычислить математическое ожидание  и дисперсию
и дисперсию  .
.
10.23. Устройство состоит из 3 независимо работающих узлов. Вероятность отказа каждого узла в течение времени  равна
равна  . Составить ряд распределения случайной величины
. Составить ряд распределения случайной величины  – числа отказов за время
– числа отказов за время  . Найти функцию распределения
. Найти функцию распределения  , построить ее график, вычислить математическое ожидание
, построить ее график, вычислить математическое ожидание  и дисперсию
и дисперсию  .
.
10.24. Вероятность попадания мячом в корзину равна  . Мяч брошен 3 раза. Построить ряд распределения случайной величины
. Мяч брошен 3 раза. Построить ряд распределения случайной величины  – числа попаданий. Найти функцию распределения
– числа попаданий. Найти функцию распределения  , построить ее график, вычислить математическое ожидание
, построить ее график, вычислить математическое ожидание  и дисперсию
и дисперсию  .
.
10.25. Вероятность попадания в цель при одном выстреле равна  . Построить ряд распределения случайной величины
. Построить ряд распределения случайной величины  – числа промахов до первого попадания при 4-х выстрелах. Найти функцию распределения
– числа промахов до первого попадания при 4-х выстрелах. Найти функцию распределения  , построить ее график, вычислить математическое ожидание
, построить ее график, вычислить математическое ожидание  и дисперсию
и дисперсию  .
.
10.26. При передаче сообщения вероятность искажения одного знака равна  . Составить ряд распределения случайной величины
. Составить ряд распределения случайной величины  – числа искаженных знаков среди 4 переданных. Найти функцию распределения
– числа искаженных знаков среди 4 переданных. Найти функцию распределения  , построить ее график, вычислить математическое ожидание
, построить ее график, вычислить математическое ожидание  и дисперсию
и дисперсию  .
.
10.27. В партии 12 деталей, среди них 5 нестандартных. Наудачу отобраны 2 детали. Составить ряд распределения случайной величины  – числа нестандартных деталей среди 2-х отобранных. Найти функцию распределения
– числа нестандартных деталей среди 2-х отобранных. Найти функцию распределения  , построить ее график, вычислить математическое ожидание
, построить ее график, вычислить математическое ожидание  и дисперсию
и дисперсию  .
.
10.28. В городе 3 библиотеки. Вероятность того, что необходимая студенту книга свободна, равна  для каждой библиотеки. Составить ряд распределения случайной величины
для каждой библиотеки. Составить ряд распределения случайной величины  – числа библиотек, которые посетит студент. Найти функцию распределения
– числа библиотек, которые посетит студент. Найти функцию распределения  , построить ее график, вычислить математическое ожидание
, построить ее график, вычислить математическое ожидание  и дисперсию
и дисперсию  .
.
10.29. Производится 4 выстрела по мишени. Вероятность попадания при каждом выстреле –  . Составить ряд распределения случайной величины
. Составить ряд распределения случайной величины  – числа промахов. Найти функцию распределения
– числа промахов. Найти функцию распределения  , построить ее график, вычислить математическое ожидание
, построить ее график, вычислить математическое ожидание  и дисперсию
и дисперсию  .
.
10.30. Устройство состоит из 3 независимо работающих узлов. Вероятность отказа каждого узла в течение времени  равна
равна  . Составить ряд распределения случайной величины
. Составить ряд распределения случайной величины  – числа узлов, которые за время
– числа узлов, которые за время  не отказали. Найти функцию распределения
не отказали. Найти функцию распределения  , построить ее график, вычислить математическое ожидание
, построить ее график, вычислить математическое ожидание  и дисперсию
и дисперсию  .
.
Задание 11. Непрерывная случайная величина.
11.1. Случайная величина  имеет плотность распределения
имеет плотность распределения  . Определить коэффициент
. Определить коэффициент  , функцию распределения
, функцию распределения  , математическое ожидание
, математическое ожидание  и дисперсию
и дисперсию  .
.
11.2. Показать, что функция  является плотностью распределения некоторой случайной величины
является плотностью распределения некоторой случайной величины  . Определить функцию распределения
. Определить функцию распределения  , математическое ожидание
, математическое ожидание  , дисперсию
, дисперсию  и вероятность попадания случайной величины
и вероятность попадания случайной величины  в промежуток
в промежуток  .
.
11.3. Случайная величина  имеет плотность распределения
имеет плотность распределения  Определить коэффициент
Определить коэффициент  , функцию распределения
, функцию распределения  , математическое ожидание
, математическое ожидание  , дисперсию
, дисперсию  и вероятность того, что случайная величина попадет в промежуток
и вероятность того, что случайная величина попадет в промежуток 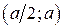 .
.
11.4. Случайная величина  имеет плотность распределения
имеет плотность распределения  Определить
Определить  , функцию распределения
, функцию распределения  , математическое ожидание
, математическое ожидание  , дисперсию
, дисперсию  и вероятность того, что случайная величина попадет в промежуток
и вероятность того, что случайная величина попадет в промежуток  .
.
11.5. Случайная величина  имеет плотность распределения
имеет плотность распределения  . Определить
. Определить  , функцию распределения
, функцию распределения  , математическое ожидание
, математическое ожидание  , дисперсию
, дисперсию  и вероятность того, что случайная величина попадет в промежуток
и вероятность того, что случайная величина попадет в промежуток  .
.
11.6. Случайная величина  имеет плотность распределения
имеет плотность распределения 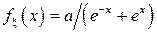 . Определить
. Определить  , функцию распределения
, функцию распределения  , математическое ожидание
, математическое ожидание  и дисперсию
и дисперсию  . Найти вероятность того, что в двух независимых испытаниях
. Найти вероятность того, что в двух независимых испытаниях  примет значения, меньшие единицы.
примет значения, меньшие единицы.
11.7. Случайная величина  имеет плотность распределения
имеет плотность распределения  . Определить
. Определить  , функцию распределения
, функцию распределения  , математическое ожидание
, математическое ожидание  и дисперсию
и дисперсию  .
.
11.8. Случайная величина  имеет плотность вероятности
имеет плотность вероятности 
 . Определить коэффициент
. Определить коэффициент  , функцию распределения
, функцию распределения  , математическое ожидание
, математическое ожидание  и дисперсию
и дисперсию  .
.
11.9. Случайная величина  имеет плотность распределения
имеет плотность распределения  Определить функцию распределения
Определить функцию распределения  , математическое ожидание
, математическое ожидание  и дисперсию
и дисперсию  .
.
11.10. Случайная величина  имеет плотность распределения
имеет плотность распределения  Определить коэффициент
Определить коэффициент  , функцию распределения
, функцию распределения  , математическое ожидание
, математическое ожидание  , дисперсию
, дисперсию  и вероятность того, что случайная величина попадет в промежуток
и вероятность того, что случайная величина попадет в промежуток  .
.
11.11.Случайная величина  имеет плотность распределения
имеет плотность распределения  Определить коэффициент
Определить коэффициент  , функцию распределения
, функцию распределения  , математическое ожидание
, математическое ожидание  , дисперсию
, дисперсию  и вероятность того, что случайная величина попадет в промежуток
и вероятность того, что случайная величина попадет в промежуток  .
.
11.12. Случайная величина  имеет плотность распределения
имеет плотность распределения  Определить коэффициент
Определить коэффициент  , функцию распределения
, функцию распределения  , математическое ожидание
, математическое ожидание  , дисперсию
, дисперсию  и вероятность того, что в трех испытаниях случайная величина
и вероятность того, что в трех испытаниях случайная величина  ровно два раза примет значение, заключенное в интервале
ровно два раза примет значение, заключенное в интервале  .
.
11.13. Дана функция  Показать, что
Показать, что 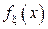 может служить плотностью распределения некоторой случайной величины
может служить плотностью распределения некоторой случайной величины  . Найти: а) дисперсию
. Найти: а) дисперсию  ; б) функцию распределения
; б) функцию распределения  ; в)
; в) 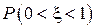 . Построить графики функций
. Построить графики функций  ,
, 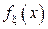 .
.
11.14. Случайная величина  имеет плотность распределения
имеет плотность распределения  Определить функцию распределения
Определить функцию распределения  , математическое ожидание
, математическое ожидание  и дисперсию
и дисперсию  .
.
11.15.Случайная величина  имеет плотность распределения
имеет плотность распределения 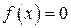 при
при  Найти: а) дисперсию
Найти: а) дисперсию  ; б) функцию распределения
; б) функцию распределения  ; в)
; в)  . Построить графики функций
. Построить графики функций  ,
, 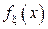 .
.
11.16. Случайная величина  задана плотностью распределения
задана плотностью распределения  . Найти: а) дисперсию
. Найти: а) дисперсию  ; б) интегральную функцию распределения
; б) интегральную функцию распределения  ; в)
; в)  . Построить графики функций
. Построить графики функций  ,
, 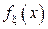 .
.
11.17. Случайная величина  задана плотностью распределения
задана плотностью распределения  Найти: а) коэффициент
Найти: а) коэффициент  и
и  ; б) дисперсию
; б) дисперсию  ; в) интегральную функцию распределения
; в) интегральную функцию распределения  . Построить графики функций
. Построить графики функций  ,
, 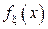 .
.
11.18. Случайная величина  задана плотностью распределения
задана плотностью распределения  Найти: а) дисперсию
Найти: а) дисперсию  ; б) интегральную функцию распределения
; б) интегральную функцию распределения  ; в)
; в)  . Построить графики функций
. Построить графики функций  ,
, 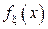 .
.
11.19. Случайная величина  задана плотностью распределения
задана плотностью распределения  Найти: а) дисперсию
Найти: а) дисперсию  ; б) интегральную функцию распределения
; б) интегральную функцию распределения  ; в)
; в)  . Построить графики функций
. Построить графики функций  ,
, 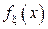 .
.
11.20. Случайная величина  задана плотностью распределения
задана плотностью распределения  Найти: а) коэффициент
Найти: а) коэффициент  и
и  ; б) дисперсию
; б) дисперсию  ; в) интегральную функцию распределения
; в) интегральную функцию распределения  . Построить графики функций
. Построить графики функций  ,
, 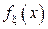 .
.
11.21. Случайная величина  задана плотностью распределения
задана плотностью распределения  для
для  . Найти: а) функцию распределения
. Найти: а) функцию распределения  ; б)
; б) 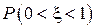 ; в) дисперсию
; в) дисперсию  . Построить графики функций
. Построить графики функций  ,
, 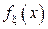 .
.
11.22. Случайная величина  задана плотностью распределения
задана плотностью распределения  Найти: а) коэффициент
Найти: а) коэффициент  и
и  ; б) дисперсию
; б) дисперсию  ; в) интегральную функцию распределения
; в) интегральную функцию распределения  . Построить графики функций
. Построить графики функций  ,
, 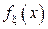 .
.
11.23. Случайная величина  задана плотностью распределения
задана плотностью распределения  Найти: а) коэффициент
Найти: а) коэффициент  и
и  ; б) дисперсию
; б) дисперсию  ; в) интегральную функцию распределения
; в) интегральную функцию распределения  . Построить графики функций
. Построить графики функций  ,
, 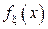 .
.
11.24. Случайная величина  задана плотностью распределения
задана плотностью распределения  Найти: а) коэффициент
Найти: а) коэффициент  и
и  ; б) дисперсию
; б) дисперсию  ; в) интегральную функцию распределения
; в) интегральную функцию распределения  . Построить графики функций
. Построить графики функций  ,
, 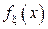 .
.
11.25. Случайная величина  задана плотностью распределения
задана плотностью распределения  Найти: а) коэффициент
Найти: а) коэффициент  и
и  ; б) дисперсию
; б) дисперсию  ; в) интегральную функцию распределения
; в) интегральную функцию распределения  . Построить графики функций
. Построить графики функций  ,
, 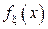 .
.
11.26. Случайная величина  задана плотностью распределения
задана плотностью распределения  Найти: а) коэффициент
Найти: а) коэффициент  и
и  ; б) дисперсию
; б) дисперсию  ; в) интегральную функцию распределения
; в) интегральную функцию распределения  . Построить графики функций
. Построить графики функций  ,
, 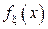 .
.
11.27. Случайная величина  задана плотностью распределения
задана плотностью распределения  ,
,  . Найти: а) коэффициент
. Найти: а) коэффициент  и
и  ; б) дисперсию
; б) дисперсию  ; в) интегральную функцию распределения
; в) интегральную функцию распределения  . Построить графики функций
. Построить графики функций  ,
, 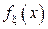 .
.
11.28. Случайная величина  задана плотностью распределения
задана плотностью распределения  Найти: а) коэффициент
Найти: а) коэффициент  и
и  ; б) дисперсию
; б) дисперсию  ; в) интегральную функцию распределения
; в) интегральную функцию распределения  . Построить графики функций
. Построить графики функций  ,
, 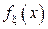 .
.
11.29. Случайная величина  задана плотностью распределения
задана плотностью распределения  Найти: а) коэффициент
Найти: а) коэффициент  и
и  ; б) дисперсию
; б) дисперсию  ; в) интегральную функцию распределения
; в) интегральную функцию распределения  . Построить графики функций
. Построить графики функций  ,
, 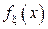 .
.
11.30. Случайная величина  задана плотностью распределения
задана плотностью распределения  Найти: а) коэффициент
Найти: а) коэффициент  и
и  ; б) дисперсию
; б) дисперсию  ; в) интегральную функцию распределения
; в) интегральную функцию распределения  . Построить графики функций
. Построить графики функций  ,
, 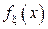 .
.

 – числа попаданий. Найти функцию распределения
– числа попаданий. Найти функцию распределения  , построить ее график, вычислить математическое ожидание
, построить ее график, вычислить математическое ожидание  и дисперсию
и дисперсию  .
. всей продукции станок-автомат выпускает первым сортом, а
всей продукции станок-автомат выпускает первым сортом, а  – вторым. Построить ряд распределения случайной величины
– вторым. Построить ряд распределения случайной величины  в 3-х независимых испытаниях, если вероятность появления события
в 3-х независимых испытаниях, если вероятность появления события  . Найти функцию распределения
. Найти функцию распределения  для каждой библиотеки. Составить ряд распределения случайной величины
для каждой библиотеки. Составить ряд распределения случайной величины  . Составить ряд распределения случайной величины
. Составить ряд распределения случайной величины  равна
равна  . Составить ряд распределения случайной величины
. Составить ряд распределения случайной величины  . Мяч брошен 3 раза. Построить ряд распределения случайной величины
. Мяч брошен 3 раза. Построить ряд распределения случайной величины  . Построить ряд распределения случайной величины
. Построить ряд распределения случайной величины  . Составить ряд распределения случайной величины
. Составить ряд распределения случайной величины  для каждой библиотеки. Составить ряд распределения случайной величины
для каждой библиотеки. Составить ряд распределения случайной величины  . Составить ряд распределения случайной величины
. Составить ряд распределения случайной величины  . Определить коэффициент
. Определить коэффициент  , функцию распределения
, функцию распределения  является плотностью распределения некоторой случайной величины
является плотностью распределения некоторой случайной величины  .
. Определить коэффициент
Определить коэффициент 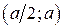 .
. Определить
Определить  .
. . Определить
. Определить  .
.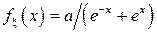 . Определить
. Определить  . Определить
. Определить 
 . Определить коэффициент
. Определить коэффициент  Определить функцию распределения
Определить функцию распределения  Определить коэффициент
Определить коэффициент  .
. Определить коэффициент
Определить коэффициент  .
. Определить коэффициент
Определить коэффициент  Показать, что
Показать, что 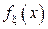 может служить плотностью распределения некоторой случайной величины
может служить плотностью распределения некоторой случайной величины 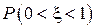 . Построить графики функций
. Построить графики функций  Определить функцию распределения
Определить функцию распределения 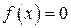 при
при  Найти: а) дисперсию
Найти: а) дисперсию  . Построить графики функций
. Построить графики функций  . Найти: а) дисперсию
. Найти: а) дисперсию  Найти: а) коэффициент
Найти: а) коэффициент  ; б) дисперсию
; б) дисперсию  Найти: а) дисперсию
Найти: а) дисперсию  . Построить графики функций
. Построить графики функций  Найти: а) дисперсию
Найти: а) дисперсию  Найти: а) коэффициент
Найти: а) коэффициент  ; б) дисперсию
; б) дисперсию  для
для  . Найти: а) функцию распределения
. Найти: а) функцию распределения  Найти: а) коэффициент
Найти: а) коэффициент  ; б) дисперсию
; б) дисперсию  Найти: а) коэффициент
Найти: а) коэффициент  Найти: а) коэффициент
Найти: а) коэффициент  ; б) дисперсию
; б) дисперсию  Найти: а) коэффициент
Найти: а) коэффициент  ; б) дисперсию
; б) дисперсию  Найти: а) коэффициент
Найти: а) коэффициент  ; б) дисперсию
; б) дисперсию  ,
,  . Найти: а) коэффициент
. Найти: а) коэффициент  ; б) дисперсию
; б) дисперсию  Найти: а) коэффициент
Найти: а) коэффициент  ; б) дисперсию
; б) дисперсию  Найти: а) коэффициент
Найти: а) коэффициент  ; б) дисперсию
; б) дисперсию  Найти: а) коэффициент
Найти: а) коэффициент  ; б) дисперсию
; б) дисперсию 


