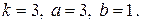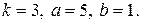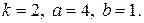Задание 15.
15.1. Задана дифференциальная функция случайной величины   в интервале в интервале  и и  вне этого интервала. Найти дифференциальную функцию вне этого интервала. Найти дифференциальную функцию  случайной величины случайной величины  . .
15.2. Случайная величина  подчинена закону равномерной плотности на интервале подчинена закону равномерной плотности на интервале  . Найти математическое ожидание и дисперсию случайной величины . Найти математическое ожидание и дисперсию случайной величины  . .
15.3. Задана плотность распределения  случайной величины случайной величины  , возможные значения которой заключены в интервале , возможные значения которой заключены в интервале  . Найти плотность распределения . Найти плотность распределения  случайной величины случайной величины  . .
15.4. Случайная величина  распределена равномерно в интервале распределена равномерно в интервале  . Найти плотность распределения . Найти плотность распределения  случайной величины случайной величины  . .
15.5. Задана плотность распределения  случайной величины случайной величины  , возможные значения которой заключены в интервале , возможные значения которой заключены в интервале  . Найти плотность распределения . Найти плотность распределения  случайной величины случайной величины  . .
15.6. Случайная величина  подчинена закону равномерной плотности на интервале подчинена закону равномерной плотности на интервале  . Найти математическое ожидание и дисперсию случайной величины . Найти математическое ожидание и дисперсию случайной величины  . .
15.7. Случайная величина  распределена по закону с плотностью распределена по закону с плотностью  в интервале в интервале  , вне интервала , вне интервала  . Найти математическое ожидание и дисперсию случайной величины . Найти математическое ожидание и дисперсию случайной величины  . .
15.8. Дискретная случайная величина  задана законом распределения: задана законом распределения:

| -1
| -2
|
|
| 
| 0,3
| 0,1
| 0,2
| 0,4
| Найти закон распределения случайной величины  . .
15.9. Случайная величина  распределена равномерно в интервале распределена равномерно в интервале  . Найти плотность распределения . Найти плотность распределения  случайной величины случайной величины  . .
15.10. Задана плотность распределения  случайной величины случайной величины  , возможные значения которой заключены в интервале , возможные значения которой заключены в интервале  . Найти плотность распределения . Найти плотность распределения  случайной величины случайной величины  . .
15.11. Случайная величина  распределена в интервале распределена в интервале  с плотностью вероятности с плотностью вероятности  . Определить плотность вероятности случайной величины . Определить плотность вероятности случайной величины  . .
15.12. Случайная величина  подчинена закону равномерной плотности на интервале подчинена закону равномерной плотности на интервале  . Найти математическое ожидание и дисперсию случайной величины . Найти математическое ожидание и дисперсию случайной величины  . .
15.13. Задана плотность распределения  случайной величины случайной величины  , возможные значения которой заключены в интервале , возможные значения которой заключены в интервале  . Найти плотность распределения . Найти плотность распределения  случайной величины случайной величины 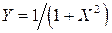 . .
15.14. Случайная величина  распределена равномерно в интервале распределена равномерно в интервале  . Найти плотность распределения . Найти плотность распределения  случайной величины случайной величины 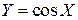 . .
15.15. Случайная величина  распределена по закону с плотностью вероятности распределена по закону с плотностью вероятности  при при  . Найти математическое ожидание и дисперсию случайной величины . Найти математическое ожидание и дисперсию случайной величины  . .
15.16. Задана плотность распределения  случайной величины случайной величины  , возможные значения которой заключены в интервале , возможные значения которой заключены в интервале  . Найти плотность распределения . Найти плотность распределения  случайной величины случайной величины  . .
15.17. Случайная величина  распределена равномерно в интервале распределена равномерно в интервале  . Найти плотность распределения . Найти плотность распределения  случайной величины случайной величины 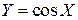 . .
15.18. Случайная величина  распределена равномерно в интервале распределена равномерно в интервале  , ,  . Найти математическое ожидание и дисперсию . Найти математическое ожидание и дисперсию  . .
15.19. Задана плотность нормально распределенной случайной величины   . Найти плотность распределения случайной величины . Найти плотность распределения случайной величины  . .
15.20. Задана плотность случайной величины  : :   . Найти плотность распределения . Найти плотность распределения  случайной величины случайной величины 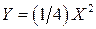 . .
15.21. Случайная величина  распределена равномерно в интервале распределена равномерно в интервале  , ,  . Найти математическое ожидание и дисперсию . Найти математическое ожидание и дисперсию  . .
15.22.Дискретная случайная величина  задана законом распределения: задана законом распределения:
Найти закон распределения случайной величины  . .
15.23. Случайная величина  подчинена закону равномерной плотности на интервале подчинена закону равномерной плотности на интервале  . Найти математическое ожидание и дисперсию случайной величины . Найти математическое ожидание и дисперсию случайной величины  . .
15.24. Задана плотность распределения  случайной величины случайной величины  , возможные значения которой заключены в интервале , возможные значения которой заключены в интервале  . Найти плотность распределения . Найти плотность распределения  случайной величины случайной величины  . .
15.25. Случайная величина  распределена равномерно в интервале распределена равномерно в интервале  , ,  . Найти математическое ожидание и дисперсию случайной величины . Найти математическое ожидание и дисперсию случайной величины  . .
15.26.Задана плотность распределения  случайной величины случайной величины  , возможные значения которой заключены в интервале , возможные значения которой заключены в интервале  . Найти плотность распределения . Найти плотность распределения  случайной величины случайной величины 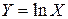 . .
15.27. Случайная величина  имеет плотность имеет плотность  при при  и и  вне интервала. Случайная величина вне интервала. Случайная величина  связана с связана с  зависимостью зависимостью  . Найти математическое ожидание и дисперсию случайной величины . Найти математическое ожидание и дисперсию случайной величины  . .
15.28. Задана плотность распределения  случайной величины случайной величины  , возможные значения которой заключены в интервале , возможные значения которой заключены в интервале  . Найти плотность распределения . Найти плотность распределения  случайной величины случайной величины  . .
15.29. Случайная величина  распределена по закону с плотностью распределена по закону с плотностью   . Найти математическое ожидание и дисперсию случайной величины . Найти математическое ожидание и дисперсию случайной величины  . .
15.30. Случайная величина  подчинена закону равномерной плотности на интервале подчинена закону равномерной плотности на интервале 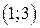 . Найти математическое ожидание и дисперсию случайной величины . Найти математическое ожидание и дисперсию случайной величины  . .
Задание 16. Дискретная 2-мерная случайная величина.
Дан совместный закон распределения двумерной случайной величины  . Найти закон распределения случайной величины . Найти закон распределения случайной величины  , математическое ожидание , математическое ожидание  и условное математическое ожидание и условное математическое ожидание  при при  . .
16.1. 


|
|
|
| 
| 0,15
| 0,2
| 0,3
| |
| 0,2
| 0,1
| 0,05
| 16.2. 


|
|
|
| |
| 0,1
| 0,5
|
| |
| 0,05
| 0,25
| 0,1
|
16.3. 
16.4. 


| 
|
|
| |
| 0,1
| 0,15
| 0,2
| |
| 0,25
| 0,1
| 0,2
|
16.5. 


| 
|
|
| 
| 0,4
| 0,15
| 0,1
| |
| 0,1
| 0,2
| 0,05
| 16.6. 
16.7. 


| 
| 
|
| |
| 0,2
| 0,1
| 0,15
| 
| 0,3
| 0,05
| 0,2
| 16.8. 


| 
|
|
| |
| 0,1
| 0,2
| 0,15
| |
| 0,25
| 0,2
| 0,1
| 16.9. 
16.10. 
16.11. 


|
|
|
| 
| 0,1
| 0,1
| 0,2
| |
| 0,25
| 0,2
| 0,15
| 16.12. 
16.13. 
16.14. 


| 
| 
|
| |
| 0,2
| 0,05
| 0,3
| |
| 0,25
| 0,1
| 0,1
| 16.15. 
16.16. 
16.17. 
16.18. 


| 
|
|
| |
| 0,1
| 0,2
| 0,15
| |
| 0,25
| 0,2
| 0,1
|
16.19. 


| 
| 
|
| 
| 0,15
| 0,1
| 0,3
| |
| 0,2
| 0,2
| 0,05
| 16.20. 


|
|
|
| 
| 0,3
| 0,1
| 0,2
| |
| 0,15
| 0,2
| 0,05
| 16.21. 


| 
|
|
| |
| 0,1
| 0,15
| 0,1
| |
| 0,3
| 0,2
| 0,15
| 16.22. 


|
|
|
| 
| 0,2
| 0,05
| 0,1
| 
| 0,1
| 0,3
| 0,25
| 16.23. 


| 
|
|
| |
| 0,1
| 0,1
| 0,15
| |
| 0,25
| 0,2
| 0,2
| 16.24. 


| 
|
|
| 
| 0,3
| 0,05
| 0,2
| |
| 0,1
| 0,2
| 0,15
|
16.25. 


| 
|
|
| |
| 0,35
| 0,1
| 0,08
| |
| 0,1
| 0,12
| 0,25
| 16.26. 


| 
|
|
| 
| 0,1
| 0,15
| 0,32
| 
| 0,25
| 0,08
| 0,1
| 16.27. 


|
|
|
| 
| 0,2
| 0,25
| 0,15
| |
| 0,05
| 0,15
| 0,2
| 16.28. 


| 
| 
|
| |
| 0,2
| 0,15
| 0,25
| |
| 0,15
| 0,1
| 0,15
| 16.29. 


| 
|
|
| 
| 0,12
| 0,05
| 0,3
| |
| 0,25
| 0,18
| 0,1
| 16.30. 


| 
|
|
| 
| 0,25
| 0,05
| 0,25
| 
| 0,1
| 0,2
| 0,15
|
Задание 17. Двумерная непрерывная случайная величина.
Плотность распределения системы случайных величин  задана формулой задана формулой 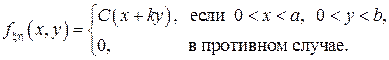
1. Найти постоянную  . .
2. Найти одномерные плотности  и и  случайных величин случайных величин  и и  . .
3. Вычислить  . .
4. Вычислить математические ожидания  , ,  , дисперсии , дисперсии 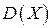 , ,  , и коэффициент корреляции , и коэффициент корреляции  . .
5. Являются ли случайные величины  и и  независимы? независимы?
| 17.1.
| 
| 17.2.
| 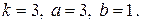
| | 17.3.
| 
| 17.4.
| 
| | 17.5.
| 
| 17.6.
| 
| | 17.7.
| 
| 17.8.
| 
| | 17.9.
| 
| 17.10.
| 
| | 17.11.
| 
| 17.12.
| 
| | 17.13.
| 
| 17.14.
| 
| | 17.15.
| 
| 17.16.
| 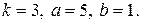
| | 17.17.
| 
| 17.18.
| 
| | 17.19.
| 
| 17.20.
| 
| | 17.21.
| 
| 17.22.
| 
| | 17.23.
| 
| 17.24.
| 
| | 17.25.
| 
| 17.26.
| 
| | 17.27.
| 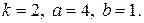
| 17.28.
| 
| | 17.29.
| 
| 17.30.
| 
|

Функция спроса населения на данный товар Функция спроса населения на данный товар: Qd=7-Р. Функция предложения: Qs= -5+2Р,где...
|

Аальтернативная стоимость. Кривая производственных возможностей В экономике Буридании есть 100 ед. труда с производительностью 4 м ткани или 2 кг мяса...
|

Вычисление основной дактилоскопической формулы Вычислением основной дактоформулы обычно занимается следователь. Для этого все десять пальцев разбиваются на пять пар...
|

Расчетные и графические задания Равновесный объем - это объем, определяемый равенством спроса и предложения...
|
Педагогическая структура процесса социализации Характеризуя социализацию как педагогический процессе, следует рассмотреть ее основные компоненты: цель, содержание, средства, функции субъекта и объекта...
Типовые ситуационные задачи. Задача 1. Больной К., 38 лет, шахтер по профессии, во время планового медицинского осмотра предъявил жалобы на появление одышки при значительной физической
Задача 1. Больной К., 38 лет, шахтер по профессии, во время планового медицинского осмотра предъявил жалобы на появление одышки при значительной физической нагрузке. Из медицинской книжки установлено, что он страдает врожденным пороком сердца....
Типовые ситуационные задачи. Задача 1.У больного А., 20 лет, с детства отмечается повышенное АД, уровень которого в настоящее время составляет 180-200/110-120 мм рт Задача 1.У больного А., 20 лет, с детства отмечается повышенное АД, уровень которого в настоящее время составляет 180-200/110-120 мм рт. ст. Влияние психоэмоциональных факторов отсутствует. Колебаний АД практически нет. Головной боли нет. Нормализовать...
|
Характерные черты немецкой классической философии 1. Особое понимание роли философии в истории человечества, в развитии мировой культуры. Классические немецкие философы полагали, что философия призвана быть критической совестью культуры, «душой» культуры.
2. Исследовались не только человеческая...
Обзор компонентов Multisim Компоненты – это основа любой схемы, это все элементы, из которых она состоит...
Кран машиниста усл. № 394 – назначение и устройство Кран машиниста условный номер 394 предназначен для управления тормозами поезда...
|
|


 в интервале
в интервале  и
и  вне этого интервала. Найти дифференциальную функцию
вне этого интервала. Найти дифференциальную функцию  случайной величины
случайной величины  .
. . Найти математическое ожидание и дисперсию случайной величины
. Найти математическое ожидание и дисперсию случайной величины  .
. случайной величины
случайной величины  . Найти плотность распределения
. Найти плотность распределения  .
. .
. .
. . Найти математическое ожидание и дисперсию случайной величины
. Найти математическое ожидание и дисперсию случайной величины  .
. в интервале
в интервале  , вне интервала
, вне интервала  . Найти математическое ожидание и дисперсию случайной величины
. Найти математическое ожидание и дисперсию случайной величины  .
.
 . Найти плотность распределения
. Найти плотность распределения  .
. . Определить плотность вероятности случайной величины
. Определить плотность вероятности случайной величины  . Найти математическое ожидание и дисперсию случайной величины
. Найти математическое ожидание и дисперсию случайной величины  .
.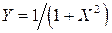 .
.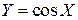 .
. при
при  . Найти математическое ожидание и дисперсию случайной величины
. Найти математическое ожидание и дисперсию случайной величины  .
. ,
,  . Найти математическое ожидание и дисперсию
. Найти математическое ожидание и дисперсию  .
. . Найти плотность распределения случайной величины
. Найти плотность распределения случайной величины  .
.
 . Найти плотность распределения
. Найти плотность распределения 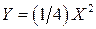 .
. . Найти математическое ожидание и дисперсию
. Найти математическое ожидание и дисперсию 


 . Найти математическое ожидание и дисперсию случайной величины
. Найти математическое ожидание и дисперсию случайной величины  .
. . Найти плотность распределения
. Найти плотность распределения  .
. . Найти математическое ожидание и дисперсию случайной величины
. Найти математическое ожидание и дисперсию случайной величины 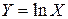 .
. при
при  и
и  . Найти математическое ожидание и дисперсию случайной величины
. Найти математическое ожидание и дисперсию случайной величины 
 . Найти математическое ожидание и дисперсию случайной величины
. Найти математическое ожидание и дисперсию случайной величины  .
.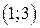 . Найти математическое ожидание и дисперсию случайной величины
. Найти математическое ожидание и дисперсию случайной величины  .
. . Найти закон распределения случайной величины
. Найти закон распределения случайной величины  , математическое ожидание
, математическое ожидание  .
.







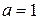







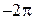

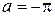
 задана формулой
задана формулой 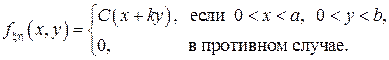
 .
. и
и  случайных величин
случайных величин  .
. ,
,  , дисперсии
, дисперсии 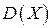 ,
,  , и коэффициент корреляции
, и коэффициент корреляции  .
.