Квазинейтральность плазмы
Характерной особенностью плазмы является ее макроскопическая нейтральность, поддерживающаяся вследствие взаимной компенсации пространственного заряда положительных ионов и электронов. Однако такая компенсация имеет место лишь в среднем – в достаточно больших объемах и за достаточно большие интервалы времени. Поэтому говорят, что плазма – квазинейтральная среда. Размеры областей и промежутки времени, в пределах которых может нарушаться компенсация объемного заряда, называют пространственным и временным масштабами разделения зарядов. Квазинейтральность плазмы предполагает выполнение в достаточно большом объеме и за достаточно длительный промежуток времени следующего условия:
где Определим пространственный масштаб разделения зарядов. Представим, что в некотором объеме плазмы нейтральность нарушена. Для простоты будем считать, что это нарушение происходит в результате смещения плоского слоя электронов. При этом образуются слои отрицательного и положительного объемных зарядов (рис. 1.3, а). Электрическое поле между слоями эквивалентно полю плоского конденсатора. Напряженность поля Е. определяется поверхностной плотностью заряда на «обкладках» и в системе СГСЭ имеет вид:
где е – заряд; nе – плотность электронов; х – толщина слоя. Распределение напряженности поля и потенциала φ показано на рис. 1.1, б, в. Полная разность потенциалов φl равна
(l – смещение слоя). Очевидно, что нарушение нейтральности, вызванное смещением слоя электронов, может поддерживаться лишь в случае, если высота потенциального барьера поля объемного заряда меньше энергии хаотического движения электронов и ионов:
где Т – меньшая из величин Те или Тi., k – постоянная Больцмана. Величина, стоящая, в правой части, определяет с точностью до численного коэффициента максимальный пространственный масштаб разделения зарядов в плазме. Эту величину, определяемую из равенства электростатической и тепловой энергий заряженных частиц, называют длиной Дебая. Точный расчет в случае электрон-протонной плазмы дает для длины Дебая выражение
Роль длины Дебая как радиуса экранирования и как пространственного масштаба разделения зарядов выражена определением плазмы Ленгмюра: совокупность свободно движущихся разноименно заряженных частиц, т.е. ионизированный газ, называется плазмой, если длина Дебая мала по сравнению с линейным размером объема, занимаемого газом. Пока радиус Дебая мал по сравнению с размером Если общее число частиц в сфере радиуса D достаточно велико для эффективной экранировки, а потенциальная энергия их взаимодействия мала в сравнении с тепловой энергией, то в термодинамическом отношении такая плазма может рассматриваться как идеальный газ. Следовательно, условие идеальности плазмы можно представить в виде
Иначе выражение (1.6) называют условием разреженности плазмы. Если увеличивать плотность плазмы, сохраняя при этом ее температуру, то согласно (1.5) величина D будет уменьшаться Определим временной масштаб разделения зарядов. Для этого обратимся снова к рис. 1.3 и рассмотрим движение электронов после нарушения нейтральности. В области нахождения электронного слоя на электроны действует сила притяжения со стороны ионов, равная
Оно описывает гармонические колебания с частотой
Нетрудно понять природу этих колебаний электронного слоя. Слой притягивается к ионному, проходит мимо него по инерции, снова притягивается и т. д. Колебания пространственного заряда при нарушении квазинейтральности были впервые обнаружены Ленгмюром. Их называют плазменными, или ленгмюровскими, колебаниями. Частоту (1.8) соответственно называют электронной плазменной, или электронной ленгмюровской, частотой. Аналогично ленгмюровские колебания ионов в плазме характеризуются ионной плазменной частотой:
Плазменной частотой принято называть величину
Поскольку
где ne измеряется в см-3. Плазменные колебания определяют механизм восстановления квазинейтральности. Очевидно, что в среднем, за много периодов колебаний, плазму можно считать нейтральной. Поэтому временной масштаб разделения зарядов в плазме определяется величиной
Его связь с пространственным масштабом разделения зарядов (1.5) очень проста:
где υ – средняя тепловая скорость электрона. Чем выше плотность плазмы, тем, согласно (1.5) и (1.12), меньше масштабы декомпенсации зарядов в пространстве и во времени. Внутри области, занятой плотной и холодной плазмой, нарушения квазинейтральности могут происходить только в пределах достаточно малых объемов. В редкой и горячей плазме дебаевская длина может оказаться значительно больше размеров области, занятой плазмой. В этом случае реализуется независимое движение электронов и ионов и отсутствует механизм для автоматического выравнивания концентраций зарядов противоположных знаков.
|

 , (1.1)
, (1.1) и
и  – усредненные концентрации ионов и электронов в плазме, z – кратность ионизации иона (z ≥ 1).
– усредненные концентрации ионов и электронов в плазме, z – кратность ионизации иона (z ≥ 1). , (1.2)
, (1.2) (1.3)
(1.3)
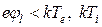 (Те и Тi – соответственно, электронная и ионная температуры плазмы, которые в общем случае могут быть различными). В противном случае движение частиц под действием электрического поля быстро приводит к восстановлению нейтральности. Подставляя в это неравенство величину φl и полагая х ≈ l, получаем
(Те и Тi – соответственно, электронная и ионная температуры плазмы, которые в общем случае могут быть различными). В противном случае движение частиц под действием электрического поля быстро приводит к восстановлению нейтральности. Подставляя в это неравенство величину φl и полагая х ≈ l, получаем 

 , (1.4)
, (1.4)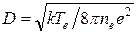 (1.5)
(1.5) На расстоянии порядка D электрическое поле отдельной частицы в плазме практически исчезает, вследствие «экранирования» частицами противоположного знака, поэтому D еще называют дебаевским радиусом экранирования.
На расстоянии порядка D электрическое поле отдельной частицы в плазме практически исчезает, вследствие «экранирования» частицами противоположного знака, поэтому D еще называют дебаевским радиусом экранирования.

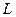 изучаемой системы L >> D, процессы нарушения квазинейтральности носят локальный и кратковременный характер. Очевидно, что это условие и условие (1.1) взаимосвязаны.
изучаемой системы L >> D, процессы нарушения квазинейтральности носят локальный и кратковременный характер. Очевидно, что это условие и условие (1.1) взаимосвязаны. . (1.6)
. (1.6) и условие (1.6) может уже не выполняться. В этом случае число частиц в сфере с радиусом D недостаточно для эффективной экранировки, и плазму уже нельзя считать идеальной. На каждую частицу начинает действовать поле остальных частиц, плазма становится, как говорят, коллективной.
и условие (1.6) может уже не выполняться. В этом случае число частиц в сфере с радиусом D недостаточно для эффективной экранировки, и плазму уже нельзя считать идеальной. На каждую частицу начинает действовать поле остальных частиц, плазма становится, как говорят, коллективной. (см.(1.2)). Уравнение движения электронов имеет вид
(см.(1.2)). Уравнение движения электронов имеет вид . (1.7)
. (1.7) . (1.8)
. (1.8) (1.9)
(1.9) (1.10)
(1.10) , то
, то  , и линейная частота плазмы определяется из выражения
, и линейная частота плазмы определяется из выражения [Гц], (1.11)
[Гц], (1.11) . (1.12)
. (1.12) , (1.13)
, (1.13)


