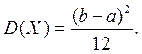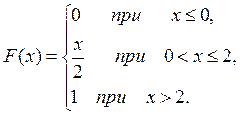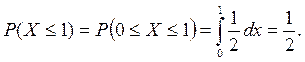НЕПРЕРЫВНОЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ

 

Введение……………………………………………………...........3

1. Равномерный закон распределения непрерывной случайной

величины…………………………………………….......……………2

2. Задачи для самостоятельного решения…………………………. 6

Контрольные вопросы…………………………………………......... 7

Литература……………………………………………………............ 7

 

 

Юлия Борисовна Егорова

Игорь Михайлович Мамонов

Татьяна Анатольевна Никулина

 

 

РАВНОМЕРНЫЙ ЗАКОН РАСПРЕДЕЛЕНИЯ

 

Методические указания к практическим занятиям

по дисциплине «Высшая математика»

 

Редактор

Подп. в печать. Уч.-изд.л. - Тираж 50 экз. Зак. №

Издательский центр МАТИ, 109240, Москва, Берниковская наб., 14

 

РАВНОМЕРНЫЙ ЗАКОН РАСПРЕДЕЛЕНИЯ

Методические указания к практическим занятиям

по дисциплине «Высшая математика»

 

Составители: Ю.Б. Егорова

И.М. Мамонов

Т.А.Никулина

 

 

МОСКВА 2011

 

 

 

Равномерный закон распределения:Методические указания к практическим занятиямпо дисциплине «Высшая математика»/ Ю.Б. Егорова, И.М. Мамонов, Т.А. Никулина. М.: МАТИ, 2011. - 8 с.

 

ÓЕгорова Ю.Б.,

Мамонов И.М.,

Никулина Т.А.

составление, 2011

 

ÓМАТИ, 2011

 

 

ВВЕДЕНИЕ

Методические указания предназначены для студентов дневного и вечернего отделений факультета №14 специальностей 150601, 160301, 220301, 230102 и направлений 080200, 150100, 160700, 220700, 230100. Большое количество рассмотренных примеров помогает в практическом освоении темы. Методические указания служат основой для практических занятий и выполнения индивидуальных заданий.

РАВНОМЕРНЫЙ ЗАКОН РАСПРЕДЕЛЕНИЯ

НЕПРЕРЫВНОЙ СЛУЧАЙНОЙ ВЕЛИЧИНЫ

 

1.1.Равномерный закон распределения имеют непрерывные случайные величины, которые могут с одинаковой вероятностью принимать любые значения из некоторого интервала числовой оси.

Примеры случайных величин, имеющих равномерный закон распределения: ошибки округлений при числовых расчетах; ошибки округлений отсчетов измерительных приборов до целых делений шкал; время ожидания какого-либо события, происходящего через определенные промежутки времени (время ожидания автобуса, поезда и т.п.) и др.

1.2. Плотность распределения вероятностей (дифференциальная функция распределения) постоянна в некотором интервале (a, b) и имеет вид:

где а и b - параметры распределения.

1.3.Интегральная функция распределения вероятностей имеет вид:

 

 

1.4.Числовые характеристики случайной величины, имеющей равномерный закон распределения:

Mатематическое ожидание:

Дисперсия:

Среднее квадратическое отклонение:

Моды Мо нет.

Медиана

Коэффициент ассиметрии А =0.

Коэффициент эксцесса e= 1,8; эксцесс Е=e– 3=-1,2.

 

1.5. Вероятность попадания в заданный интервал. Вероятность того, что случайная величина Х, имеющая равномерный закон распределения, попадет в заданный интервал (a,b), равна:

или

 

ПРИМЕР 1. Поезда метрополитена идут регулярно с интервалом 2 мин. Пассажир выходит на платформу в случайный момент времени. Время ожидания поезда – это непрерывная случайная величина (НСВ) Х, имеющая равномерный закон распределения вероятностей. Найти интегральную и дифференциальную функции распределения НСВ Х. Определить числовые характеристики случайной величины Х. Найти вероятность того, что пассажиру придется ждать поезда не более минуты.

Решение.

НСВ Х – время ожидания поезда – может принять любое значение в интервале от 0 до 2 мин (a =0, b= 2).

Плотность распределения вероятностей (дифференциальная функция распределения) имеет вид:

Интегральная функция распределения вероятностей имеет вид:

Числовые характеристики НСВ Х:

Математическое ожидание:

Дисперсия:

Среднее квадратическое отклонение:

Моды Мо нет.

Медиана

Определим вероятность того, что пассажиру придется ждать поезда не более одной минуты:

или

 

ПРИМЕР 2. Цена деления шкалы амперметра равна 0,1 А. Показания прибора округляют до ближайшего целого числа (деления). Ошибка округления распределена по равномерному закону. Найти вероятность того, что при отсчете будет сделана ошибка, превышающая 0,02 А.

 

Решение. НСВ Х –ошибка округления – может принять любое значение в интервале от 0 до 0,1 А (a =0, b= 0,1).

Плотность распределения вероятностей (дифференциальная функция распределения) имеет вид:

Интегральная функция распределения вероятностей имеет вид:

Ошибка отсчета превысит 0,02, если она будет заключена в интервале от 0,02 до 0,08 А. Тогда вероятность того, что при отсчете будет сделана ошибка, превышающая 0,02 А:

или