Температурное поле в плоской стенке при граничных условиях первого рода.

 

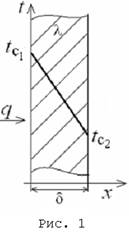
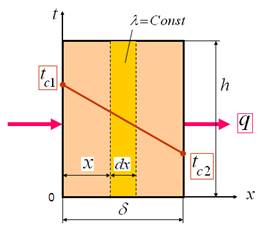
При установившемся или стационарном тепловом режиме температура тела не зависит от времени. Рассмотрим однородную и изотропную стенку (рис. 1) толщиной d с постоянным коэффициентом теплопроводности λ. На наружных поверхностях стенки поддерживаются постоянными температуры t_c1 и t_c2. Обозначим:

Dt=t-t_c2 – текущий температурный напор или избыточная температура;

Dt₀=t_c1-t_c2 – полный температурный напор или наибольшая избыточная температура.

Дифференциальное уравнение теплопроводности

(2)

где -оператор Лапласа,

для рассматриваемого случая (внутренние источники тепла отсутствуют q_v=0, тепловой режим стационарный ) запишется в виде

Закон распределения температуры по толщине стенки найдем, дважды проинтегрировав уравнение (1) и найдя константы интегрирования из граничных условий, заданных уравнениями (2):

 

 

Для определения количества тепла, проходящего через единицу поверхности стенки в единицу времени в направлении оси Ох, воспользуемся законом Фурье, согласно которому

(12)

Из уравнения (12) следует, что количество тепла, проходящее через единицу поверхности в единицу времени прямо пропорционально коэффициенту теплопроводности и температурному напору и обратно пропорционально толщине стенки. Отношение λ/d называется тепловой проводимостью стенки, а обратная величина d / λ; – тепловым или термическим сопротивлением стенки.

Последнее представляет собой падение температуры в стенке на единицу плотности теплового потока. Зная удельный тепловой поток, легко вычислить общее количество тепла, которое передается через поверхность стенки величиной F за промежуток времени t:

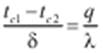Из уравнения (12) найдем величину перепада температуры на длину стенки и подставим ее в уравнение (9а):

. (13)