Эквивалентный коэффициент теплопроводности плоской стенки
Рассмотрим теплопроводность многослойной стенки (рис. 3), состоящей из n однородных слоев. Примем, что контакт между слоями совершенный и температура на соприкасающихся поверхностях двух слоев одинакова. При стационарном режиме тепловой поток, проходящий через любую изотермическую поверхность неоднородной стенки, один и тот же, т.е.
При заданных температурах внешних поверхностей такой стенки, размерах слоев и, соответственно, коэффициентах теплопроводности можно составить систему уравнений для плотности теплового потока каждого из слоев, из которых выразим температурные напоры:
Сложив левые и правые части уравнений, получим:
Отсюда плотность теплового потока
Величина Температуры на границе соприкосновения двух соседних слоев равны:
Внутри каждого из слоев температура изменяется согласно уравнениям (2.3), (2.5) или (2.7), а для многослойной стенки в целом температурная кривая представляет ломаную линию. При сравнении переноса тепла через многослойную стенку и стенку из однородного материала удобно ввести в рассмотрение эквивалентный коэффициент теплопроводности для многослойной стенки λэкв. Он равен коэффициенту теплопроводности однородной стенки, толщина которой D равна толщине многослойной стенки
Отсюда получаем:
Таким образом, эквивалентный коэффициент теплопроводности λэкв зависит не только от теплофизических свойств слоев, но и от их толщины.
|

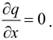




 , равная сумме тепловых сопротивлений всех n слоев, называется полным тепловым или термическим сопротивлением теплопроводности многослойной стенки.
, равная сумме тепловых сопротивлений всех n слоев, называется полным тепловым или термическим сопротивлением теплопроводности многослойной стенки.
 , а тепловое сопротивление равно термическому сопротивлению рассматриваемой многослойной стенки, т. е.
, а тепловое сопротивление равно термическому сопротивлению рассматриваемой многослойной стенки, т. е.




