Методические указания. для студентів напряму «Телекомунікації» (ІІІ курс, VI семестр)
для студентів напряму «Телекомунікації» (ІІІ курс, VI семестр)
Склав: доцент, к.ф.-м.н. Плешівський Я.М.
м.Львів-2014 р.
1. Перетворення Лапласа. Оригінали та зображення. 2. Властивості зображень Лапласа (теореми про лінійність, зміщення, подібність). 3. Властивості зображень Лапласа (теореми запізнення, диференціювання оригіналу, диференціювання зображення). 4. Властивості зображень Лапласа (теореми про інтегрування оригіналу, множення зображень). 5. Визначення оригіналу за його зображенням Лапласа. 6. Визначення та геометричне зображення комплексних чисел. 7. Алгебраїчна форма запису комплексних чисел, приклади. 8. Тригонометрична форма запису комплексних чисел, приклади. 9. Показникова форма запису комплексних чисел, приклади. 10. Дії з комплексними числами в алгебраїчній формі. 11. Дії з комплексними числами в тригонометричній формі. 12. Дії з комплексними числами в показниковій формі. 13. Поняття функції комплексної змінної, приклади. 14. Регулярність функції комплексної змінної. 15. Умови Коші-Рімена функцій комплексної змінної. 16. Поняття цілої функції комплексної змінної. 17. Поняття порядку росту функції комплексної змінної. 18. Ряд Лорена функції комплексної змінної. 19. Типи особливих точок функцій комплексної змінної. 20. Ряд Лорена функції комплексної змінної. 21. Значення головної та правильної частини ряду Лорена функції комплексної змінної. 22. Інтегральні лишки функції комплексної змінної. 23. Обчислення інтегральних лишків функції комплексної змінної та їх зв’язок з розкладом в ряд Лорена. 24. Визначення оригіналу за його зображенням Лапласа, таблиця зображень. 25. Геометрична інтерпретація комплексних чисел. 26. Функції комплексної змінної, основні означення і поняття. 27. Границя та неперервність функції комплексної змінної. 28. Основні трансцендентні функції комплексної змінної. 29. Функціональні та степеневі ряди функцій комплексної змінної. 30. Ряд Тейлора функцій комплексної змінної.
1. Визначення та геометричне зображення комплексних чисел. 2. Записати в тригонометричній формі число: 3. Тригонометрична форма запису комплексних чисел, приклади. 4. Записати в тригонометричній формі число: 5. Дії з комплексними числами в алгебраїчній формі. 6. Представити у показниковій формі число: 7. Виконати дії: 8. Поняття функції комплексної змінної, прилади. 9. Виконати дії: 10. Поняття порядку росту функції комплексної змінної. 11. Ряд Лорена функції комплексної змінної. 12. Типи особливих точок функцій комплексної змінної. 13. Дії з комплексними числами в тригонометричній формі. 14. Дії з комплексними числами в показниковій формі. 15. Представити в тригонометричній і показниковій формах число 16. Виконати дії: 17. Виконати дії: 18. Перевести в показникову і тригонометричну форми числа: 19. Інтегральні лишки функції комплексної змінної. 20. Знайти зображення Лапласа для функції оригіналу 21. Властивості перетворення Лапласа. 22. Представити в показниковій формі число: 23. Визначення оригіналу за його зображенням Лапласа, таблиця зображень. 24. Записати в показниковій формі число: 25. Виконати дії: 26. Виконати дії: 27. Виконати дії: 28. Виконати дії: 29. Виконати дії: 30. Виконати дії:
1. Розв’язання задач Коші для диференціальних рівнянь операційним методом. 2. Основні поняття комбінаторики (розміщення, перестановки, комбінації). 3. Поняття про випробування і події. Дії над подіями. 4. Розв’язання задачі Коші для диференціального рівняння операційним методом. 5. Основні поняття комбінаторики (розміщення, перестановки, комбінації). 6. Поняття про випробування і події. Дії над подіями. 7. Означення ймовірності випадкової події. Теореми про ймовірність суми і добутку несумісних та незалежних подій. 8. Означення ймовірності випадкової події. Теореми ймовірності суми і добутку сумісних та залежних подій. 9. Формула повної ймовірності. 10. Формула Байєса. 11. Формула повної ймовірності. 12. Формула Байєса. 13. Формула Бернулі. 14. Дії над подіями та їх ймовірностями (теорема додавання ймовірностей несумісних подій). 15. Дії над подіями та їх ймовірностями (теорема додавання ймовірностей сумісних подій). 16. Теореми множення ймовірностей залежних та незалежних подій. 17. Формула повної ймовірності. 18. В першому ящику 8 білих і 6 чорних куль, а в другому – 10 білих і 4 чорних. Навмання вибирають і ящик і кулю. Відомо, що вийнята куля чорна. Знайти ймовірність того, що було вибрано перший ящик. 19. Ймовірність влучення в ціль з одного пострілу 0,8. Яка ймовірність влучити в ціль 7 разів з 10 пострілів? 20. Ймовірність вдалого з’єднання абонентів при одному виклику 0,9. Яка ймовірність вдалих з’єднань 8 разів з 10 викликів? 21. Обчислити: 22. Обчислити: 23. Обчислити: 24. Перевірити: 25. Скількома способами можна скласти список з 10 чоловік? 26. Поняття функцій-оригіналів та зображення Лапласа. 27. Властивості зображення Лапласа. 28. Визначення оригіналу за його зображенням Лапласа, таблиця зображень. 29. Формула повної ймовірності. 30. Формула Байєса.
1. Знайти значення кореня 2. Знайти значення кореня 3. Знайти значення кореня 4. Знайти значення кореня 5. Знайти значення кореня 6. Визначити типи особливих точок функції 7. Визначити типи особливих точок функції 8. Визначити типи особливих точок функції 9. Визначити типи особливих точок функції 10. Визначити типи особливих точок функції 11. Знайти лишок функції 12. Знайти лишок функції 13. Знайти лишок функції 14. Знайти лишок функції 15. Знайти лишок функції 16. Знайти зображення Лапласа функції 17. Знайти зображення Лапласа функції 18. Знайти зображення Лапласа функції 19. Знайти зображення Лапласа функції 20. Знайти зображення Лапласа функції 21. Методом операційного числення знайти розв’язок задачі Коші 22. Методом операційного числення знайти розв’язок задачі Коші 23. Методом операційного числення знайти розв’язок задачі Коші 24. Методом операційного числення знайти розв’язок задачі Коші 25. В урні 9 білих, 15 чорних, 20 червоних та 5 блакитних кульок однакового розміру. Навмання взято одну кулю. Знайти ймовірність того, що куля буде: а) біла або червона; б) біла, чорна або блакитна. 26. В урні 12 білих, 14 чорних, 22 червоних та 6 блакитних куль однакового розміру. Навмання взято одну кулю. Знайти ймовірність того, що куля буде: а) біла або червона; б) біла, чорна або блакитна. 27. Ймовірність того, що напруга в електричній мережі стане вищою за номінальну, дорівнює 1/8. Коли напруга збільшується, ймовірність аварії приладу споживача електроенергії дорівнює 1/7. Визначити ймовірність аварії приладу внаслідок збільшення напруги. 28. Знайти вибіркову середню та вибіркову дисперсію заданої вибірки
29. Знайти вибіркову середню та вибіркову дисперсію заданої вибірки
30. Таблиця перетворення Лапласа. Методические указания
|

 .
. .
. .
.
 де
де 
 .
. , де
, де 
 .
. .
.
 .
. ;
;  де
де  .
.
 .
. .
.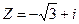 .
.
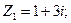
 .
. ;
; 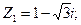
 .
.

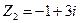 .
. .
. ;
;  де
де 
 .
. .
.
 .
.
 .
. .
. ;
;  .
. .
. .
. .
. .
. .
.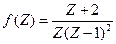 .
. .
. .
. .
. .
. відносно полюса
відносно полюса 
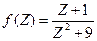 ,
,  .
. ,
,  .
. ,
,  ,
,  .
. ,
, 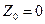 .
. .
. .
. .
. .
. .
.

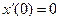 .
.

 .
.



