Подобие лопастных нагнетателей
Сложность гидро и аэродинамических процессов, происходящих в рабочем колесе лопастного нагнетателя, делает невозможным расчет его характеристики. Поэтому она строится только экспериментально. Теория подобия позволяет, выбрав существующий (модельный) нагнетатель с известной характеристикой, рассчитать характеристику проектируемого (натурного) нагнетателя. Пересчет характеристик по плотности, частоте вращения вала и диаметру рабочего колеса основан на теории гидродинамического подобия, которая требует выполнения трех условий. Геометрическое подобие, согласно которому необходимо существование пропорциональности соответствующих размеров нагнетателя. Пусть имеется натурный нагнетатель, диаметр колеса которого D2н, ширина колеса b2н и так далее. Все параметры, характеризующие работу натурной машины (на которой по тем или иным причинам мы не можем провести эксперимент), будут иметь индекс «н». Параметры модельного нагнетателя будем обозначать индексом «м». Тогда условие геометрического подобия запишется в виде b1н / b1м = D1н / D1м = … = b2н / b2м = D2н / D2м = … =idem. (1) Индекс «1» относится к входу в рабочее колесо, а индекс «2» к выходу. Кинематическое подобие, которое предусматривает подобие треугольников скоростей в сходственных точках потока. Это означает, что мы имеем право записать для относительных W, окружных U, абсолютных C скоростей и их проекций при входе и выходе из колеса соотношение: W1н / W1м = C1н / C1м = … = U1н / U1м = W2н / W2м = = C2н / C2м = … =U2н / U2м = woн R2н / woм R2м = idem,(2) где wo- угловая скорость вращения вала колеса нагнетателя связана с частотой вращения вала n соотношением wo= 2 p n и окружной скоростью U2 = wo R2. Из кинематического подобия следует равенство углов установки лопаток на входе и выходе из рабочего колеса b2н = b2м; b1н = b1м. (3) Динамическое подобие, которое предусматривает подобие сил в сходственных точках потока. Из динамического подобия следует равенство КПД натуры и модели (hн = hм). Геометрическое и кинематическое подобие осуществляется легко. Динамическое подобие осуществляется труднее, а иногда совсем не осуществимо. Например, динамическое подобие сил инерции и вязкости требует, чтобы числа Рейнольдса были одинаковы для натуры и модели: Reн = Vнdн/nн = Vмdм/n м = Reм. (4) Если размеры модели уменьшить в десять раз, а скорости в пять раз, то для динамического подобия необходимо выбрать модельную жидкость, вязкость которой в пятьдесят раз меньше вязкости натурной жидкости. А таких жидкостей в природе нет, поэтому в этом случае динамическое подобие не осуществимо. Но в некоторых случаях гидродинамические процессы не зависят от некоторых сил. Например, при больших числах Рейнольдса потери напора не зависят от сил вязкости (на практике это встречается при движении воздуха в вентиляционных системах или при движении воды в водопроводных трубах), поэтому динамическое подобие по силам вязкости можно не требовать. Но при движении жидкостей с большой вязкостью, если не выполняется динамическое подобие необходимо пересчитывать КПД нагнетателя. Подача нагнетателя определяется выражением: для вентилятора L = w2 c2r = p D2 b2 c2r,(5) где w2 – площадь выходного сечения колеса нагнетателя; D2 – диаметр выходного сечения; b2 – ширина выходного сечения; c2r – радиальная составляющая скорости. Отношение подач натурного и модельного нагнетателей составит для вентилятора с учетом первого (1) и второго (2) условиями гидродинамического подобия:
Для определения формул пересчета давлений воспользуемся уравнением Эйлера.
В этом случае отношение давлений натурного и модельного нагнетателей равно в соответствии с условием (2):
Для получения формул пересчета мощности воспользуемся выражением:
Отношения подач и напоров определены известными выражениями (7) и (8), поэтому формула пересчета мощности примет вид:
Формулы пересчета подачи (6), давления (напора) (8) и мощности (10), полученные на основе теории подобия, позволяют пересчитывать параметры, определяющие работу нагнетателей при изменении угловой скорости вращения колеса нагнетателя wo (или по частоте вращения вала n), диаметра рабочего колеса и плотности перемещаемой среды, а также характеристики натурных нагнетателей, полученные на модельных установках. Напор насоса H связан с полным давлением соотношением P = r g H. Подача насосов обозначается Q. Тогда формулы пересчета примут вид:
Коэффициент быстроходности ns. В настоящее время широко применяется метод проектирования новых нагнетателей путем пересчета по формулам подобия. Для пользования этим методом необходимо разработать параметр, который служил бы критерием подобия, который не зависел бы от диаметра колеса и был бы одинаков для всех подобных нагнетателей. Критерий подобия не имеет размерности, поэтому из размерных параметров нагнетателя давления P, производительности L, плотности жидкости r и частоте вращения вала n можно составить следующую безразмерную комбинацию, которую и можно назвать коэффициентом быстроходности:
где c – постоянное безразмерное число. Исторически сложилось так, что для насосов и вентиляторов это число выбиралось разным. Поэтому формула (15) для вентилятора при стандартных условиях (r = 1,2 кг/м3) примет вид
Для насосов P = r g H. Подставляя численное значение g в (16) получим
В этих формулах частота вращения вала n подставляется в об/мин, а угловая скорость вращения вала wo – рад/сек. Иногда для насосов коэффициентом быстроходности называют такую частоту вращения геометрически подобного насоса, который при напоре Н = 1 м имеет подачу Q = 0,075 м3/с при максимальном КПД. Коэффициент быстроходности для подобных нагнетателей одинаков и не зависит ни от диаметра колеса, ни от частоты вращения. Для центробежных насосов ns < 80, для радиальных вентиляторов ns = 6 - 120 и для осевых вентиляторов ns = 120 - 300. Пользоваться полными характеристиками, несмотря на их простоту и наглядность, не совсем удобно, поскольку каждая полная характеристика соответствует только одной частоте вращения рабочего колеса. Поэтому для подбора нагнетателей преимущественное распространение получили универсальные характеристики, которые могут быть индивидуальными, совмещенными и безразмерными. Индивидуальной характеристикой называется характеристика нагнетателя, построенная для различных частот вращения (угловых скоростей) рабочего колеса. Эти характеристики могут быть получены путем пересчета исходной характеристики нагнетателя на другие частоты вращения колеса с помощью приведенных выше формул пересчета при постоянном диаметре колеса и плотности перекачиваемой жидкости (воздуха). Индивидуальные характеристики строятся в координатах P – L (Рис. 1) или в координатах ℓg P – ℓg L (Рис. 2). Кроме самих характеристик на рисунках проводят линии равных КПД. В первом случае линии равных КПД имеют вид парабол, а во втором случае – прямые линии. Иногда на индивидуальной характеристике выделяют штриховкой область оптимальных режимов или строят только эту область. Совмещенной характеристикой называется совокупность индивидуальных характеристика подобных нагнетателей построенных для различных типоразмеров нагнетателя (различных значений диаметра рабочего колеса). Эти характеристики строятся в координатах P – L (Рис. 3). Но более удобны для подбора вентилятора совмещенные характеристики в логарифмических координатах ℓg P – ℓg L (Рис. 4). На этих характеристиках проводят дополнительные линии равного диаметра колеса, (№ вентилятора) и линию равных частот вращения колеса (или равных угловых скоростей вращения вала). Безразмерные характеристики строят по типу индивидуальных, но в безразмерных координатах. Вводятся следующие безразмерные параметры: коэффициент подачи j
коэффициент полного y, статического ys и динамического yd давления:
коэффициент мощности l
КПД рассчитывается по формуле h = y j / l и строят графики зависимости y = y(j), l = l(j), h = h(j). Безразмерные характеристик для подобных нагнетателей одинаковы и не зависят от размеров нагнетателя частоты вращения и плотности (Рис. 5).
|

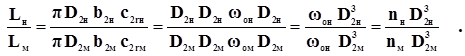 (6)
(6)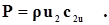 (7)
(7)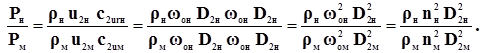 (8)
(8)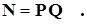 (9)
(9)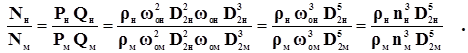 (10)
(10)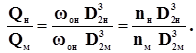 (11)
(11)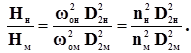 (12)
(12)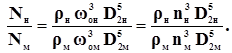 (13)
(13)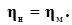 (14)
(14)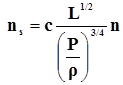 ,(15)
,(15)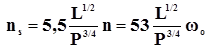 ,(16)
,(16)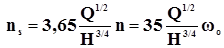 ,(17)
,(17)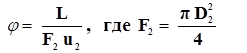 ;(18)
;(18)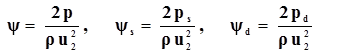 ;(19)
;(19)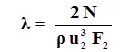 .(20)
.(20)


