Уравнение волны. Уравнение плоской гармонической волны. Волновое уравнение. Уравнение сферической волны
Уравнением упругой волны называют функцию Выведем уравнение плоской гармонической волны, распространяющейся в положительном направлении оси Для гармонической волны все частицы среды совершают колебания с одинаковой циклической частотой
Частицы с координатой х начнут совершать ГК только после прихода к ним волны. Для этого требуется время
Уравнение (6.3) представляет собой уравнение плоской гармонической волны, распространяющейся в положительном направлении оси
Волновое число к представляет собой модуль волнового вектора Покажем, что входящая в формулу (6.3) фазовая скорость
что согласуется с формулой (6.4). Волновым уравнением называют уравнение, решением которого является уравнение волны
тогда волновое уравнение примет вид
Оказывается, что решением этого уравнения, кроме плоской гармонической волны, бегущей в положительном направлении оси
Для плоской гармонической волны, распространяющейся в произвольном направлении, которое можно задать радиус-вектором
Можно показать, что волновому уравнению (6.7) удовлетворяет также и уравнение сферической волны
Это уравнение отличается от уравнения плоской гармонической волны тем, что для сферической волны амплитуда А будет зависеть от расстояния r между точечным источником колебаний и рассматриваемой точкой пространства, а именно, амплитуда сферической волны убывает обратно пропорционально расстоянию r. Действительно, амплитуда колебаний частиц среды определяется энергией W волны, приходящейся на единицу поверхности фронта волны (площадь поверхности фронта волны равна А ~ В заключение этого параграфа рассмотрим ряд примеров, поясняющих распространение плоской гармонической волны (6.3) в положительном направлении оси Пример 1. Записать уравнение колебаний для смещения Подставляя в формулу (6.3) значение
график этой зависимости представлен на рис. 6.5, а.
Рис. 6.5 Пример 2. Записать уравнение, описывающее положения всех частиц среды около своих положений равновесия в момент времени t=Т/2 при начальной фазе колебаний источника Подставляя в формулу (6.3) значение
график этой зависимости представлен на рис. 6.5, б. Из него следует, что периодом по координате является длина волны λ, т.е. через расстояние вдоль скорости распространения волны, равное длине волны λ, повторяются смещения частиц относительно своих положений равновесия. Пример 3. Найти разность фаз Согласно уравнению (6.3), запишем
Пример 4. Рассчитать отношение максимальной скорости Используя для максимальной скорости
т.е. для волн звуковой частоты скорость распространения колебаний в воздухе значительно превосходит максимальную скорость колебаний частиц воздуха.
|

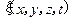 , которая определяет смещение любой частицы среды с координатами
, которая определяет смещение любой частицы среды с координатами  относительно своего положения равновесия в произвольный момент времени t. В общем случае уравнение волны определяет зависимость от координат и времени величин, описывающих волновой процесс, как для упругих волн, так и для электромагнитных волн. Часто функцию
относительно своего положения равновесия в произвольный момент времени t. В общем случае уравнение волны определяет зависимость от координат и времени величин, описывающих волновой процесс, как для упругих волн, так и для электромагнитных волн. Часто функцию  . Как известно, в плоскости фронта волны (в плоскости
. Как известно, в плоскости фронта волны (в плоскости  и параллельных ей плоскостях) все частицы среды совершают колебания в одинаковой фазе, поэтому в уравнении волны будет отсутствовать зависимость от координат у и z:
и параллельных ей плоскостях) все частицы среды совершают колебания в одинаковой фазе, поэтому в уравнении волны будет отсутствовать зависимость от координат у и z:  .
. . Пусть в момент времени
. Пусть в момент времени  частицы среды с координатой
частицы среды с координатой  , расположенные в плоскости
, расположенные в плоскости 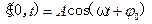 . (6.2)
. (6.2)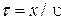 и поэтому уравнение колебаний для таких частиц примет вид:
и поэтому уравнение колебаний для таких частиц примет вид: . (6.3)
. (6.3)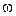 , фазовой скоростью υ волны и ее пространственным периодом λ соотношением
, фазовой скоростью υ волны и ее пространственным периодом λ соотношением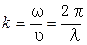 . (6.4)
. (6.4) . Направление волнового вектора
. Направление волнового вектора 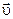 волны представляет собой скорость движения фиксированного значения фазы волны. Действительно,
волны представляет собой скорость движения фиксированного значения фазы волны. Действительно,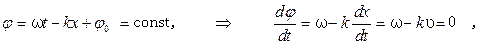
 , (6.5)
, (6.5) . Найдем волновое уравнение для волновой функции (6.3). Если взять частные производные по координате
. Найдем волновое уравнение для волновой функции (6.3). Если взять частные производные по координате  и времени t от
и времени t от  ,
, 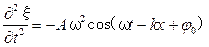 ,
, ,
,  ,
, . (6.6)
. (6.6)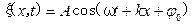 .
. , уравнение волны и волновое уравнение запишутся следующим образом
, уравнение волны и волновое уравнение запишутся следующим образом , (6.7)
, (6.7)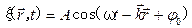 . (6.8)
. (6.8) (6.9)
(6.9)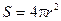 ) вблизи рассматриваемой точки, и поэтому
) вблизи рассматриваемой точки, и поэтому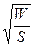 ~
~  ~
~  .
. частицы среды с координатой
частицы среды с координатой  , равной
, равной  (
( ), около своего положения равновесия в зависимости от времени t (начальную фазу колебаний источника взять равной нулю:
), около своего положения равновесия в зависимости от времени t (начальную фазу колебаний источника взять равной нулю:  ). Построить график этой зависимости в пределах одного периода.
). Построить график этой зависимости в пределах одного периода.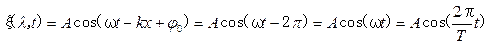 ,
,
 , получим
, получим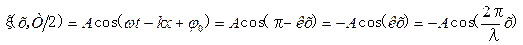 ,
, колебаний двух частиц среды, отстоящих от источника колебаний на расстоянии
колебаний двух частиц среды, отстоящих от источника колебаний на расстоянии  и
и  соответственно.
соответственно. .
. колебаний частиц воздуха к скорости
колебаний частиц воздуха к скорости 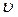 звуковой волны (
звуковой волны ( ,
,


