Характеристики волновых процессов
Под упругой средой понимают среду, между частицами которой действуют упругие силы. Если какую-либо частицу среды заставить совершать колебания, то за счет действия упругих сил в колебательное движение приходят сначала ближайшие к ней соседние частицы, затем ближайшие к этим соседям частицы и т.д., в колебательный процесс вовлекаются все новые и новые частицы, говорят, что в среде распространяется упругая волна. Итак, под бегущей волной понимают процесс распространения колебаний в среде. Этот процесс сопровождается переносом энергии от источника колебаний, причем переноса частиц в направлении движения волны не происходит, они совершают колебания около своих положений равновесия. Нужно отметить, что под частицей среды понимают не отдельную молекулу, а совокупность большого числа молекул, обладающих примерно одинаковыми свойствами (одинаковыми смещениями от своих положений равновесия, одинаковыми скоростями и т.д.). Размеры частиц должны быть достаточно малыми, значительно меньше возмущений, возникающих в среде, в частности, значительно меньше длины волны, распространяющейся в среде. Такие частицы препятствуют различным деформациям и, таким образом, среда проявляет упругие свойства. Молекулярное строение среды при этом не рассматривается, она считается сплошной. Различают продольные и поперечные волны. В продольной волне частицы среды совершают колебания вдоль вектора скорости распространения волны, а в поперечной волне – перпендикулярно к нему (рис. 6.1, а).
Рис. 6.1 Продольные волны связаны с деформациями сжатия и растяжения малых объемов среды (рис. 6.1, а), и поэтому они распространяются во всех средах. В отличие от продольных волн поперечные волны связаны с деформацией сдвига (рис. 6.1, б), поэтому они распространяются только в твердых телах, так как для жидкостей или газов такая деформация отсутствует. Отметим, что кроме волн в упругой среде также выделяют волны на поверхности жидкости, здесь частицы среды совершают сложные колебания, включающие в себя и поперечные и продольные движения. Введем характеристики, описывающие волновой процесс, на примере гармонической (синусоидальной) волны. Гармонической (синусоидальной) волной называют волну, для которой частицы среды совершают гармонические колебания около своих положений равновесия с определенной циклической частотой
Эти фотографии дают в эти моменты времени смещения Рис. 6.2 частица 1 будет максимально отклонена от своего положения равновесия, ее смещение равно амплитуде колебания Из рис. 6.2 видно, что чем дальше частица отстоит от источника колебаний, тем больше она запаздывает в совершении колебаний по сравнению с источником колебаний.
1. Период Т волны – время одного полного колебания частиц среды. 2. Фазовая скорость Рис. 6.3 3. Длина
с разностью фаз, равной
4. Волновая поверхность - поверхность, проведенная через равновесные положения частиц среды, совершающих колебания в одинаковой фазе (на Рис. 6.3 приведены волновые поверхности для плоской гармонической волны). Волновых поверхностей много, и они неподвижны. 5. Фронт волны - поверхность, разделяющая частицы среды на вовлеченные и не вовлеченные в колебательное движение. Фронт волны один, и он движется со скоростью волны. Можно сказать, что фронт волны – это самая дальняя от источника колебаний в данный момент времени волновая поверхность. В каждой точке фронта волны вектор фазовой скорости направлен перпендикулярно к ней. Форма волновых поверхностей и фронта волны зависит от условий возникновения и распространения волны. По виду фронта волны выделяют плоские, сферические, и цилиндрические волны (рис. 6.4). Для этих волн источником колебаний являются соответственно плоскость, точка и протяженная нить.
Рис. 6.4
|


 .
. Рассмотрим процесс возникновения в среде поперечной плоской гармонической волны. Пусть в момент времени
Рассмотрим процесс возникновения в среде поперечной плоской гармонической волны. Пусть в момент времени  все частицы в плоскости
все частицы в плоскости  (для этой плоскости координата
(для этой плоскости координата 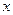 равна нулю-
равна нулю-  ) начинают совершать гармонические колебания с периодом колебаний
) начинают совершать гармонические колебания с периодом колебаний  . На рис. 6.2 для частиц, расположенных на оси
. На рис. 6.2 для частиц, расположенных на оси 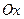 , показаны фотографии волны в моменты времени
, показаны фотографии волны в моменты времени  и
и  частиц среды около своих положений равновесия. Так, например, в момент времени
частиц среды около своих положений равновесия. Так, например, в момент времени 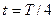
 , при этом волна за это время проходит расстояние до частицы с номером 3. В момент времени
, при этом волна за это время проходит расстояние до частицы с номером 3. В момент времени  , частица 1 проходит положение равновесия
, частица 1 проходит положение равновесия  , частица 3 максимально отклонена вверх
, частица 3 максимально отклонена вверх  , волна доходит до частицы с номером 5. В момент времени
, волна доходит до частицы с номером 5. В момент времени  волна достигает частицы с номером 9 и расстояние, пройденное волной за это время, называют длиной волны и обозначают символом
волна достигает частицы с номером 9 и расстояние, пройденное волной за это время, называют длиной волны и обозначают символом  .
. Учитывая приведенные выше фотографии распространения плоской поперечной гармонической волны в среде, можно дать следующие определения основных характеристик волнового процесса.
Учитывая приведенные выше фотографии распространения плоской поперечной гармонической волны в среде, можно дать следующие определения основных характеристик волнового процесса. волны или скорость распространения волны – скорость перемещения данной фазы колебаний в среде.
волны или скорость распространения волны – скорость перемещения данной фазы колебаний в среде. волны - расстояние, которое проходит волна за один период или минимальное расстояние между частицами среды, совершающими колебания
волны - расстояние, которое проходит волна за один период или минимальное расстояние между частицами среды, совершающими колебания . Из определения длины волны можно записать следующую формулу:
. Из определения длины волны можно записать следующую формулу: . (6.1)
. (6.1)



