Нормальные колебания (моды). Связанные колебательные системы
Под нормальными колебаниями (нормальными модами) понимают собственные (свободные) незатухающие гармонические колебания в замкнутых линейных колебательных системах (в них отсутствуют как потери энергии, так и приток извне колебательной энергии). Каждое нормальное колебание характеризуется определенным значением частоты. Эти частоты называются собственными частотами системы. Вводится понятие степеней свободы системы. Под степенями свободы системы понимают число независимых параметров, описывающих возможные изменения состояния системы. Линейные колебательные системы (они представляют собой гармонические осцилляторы, такие как колебательный контур, пружинный маятник, математический маятник) являются системами с одной степенью свободы. Действительно, для описания их движения необходимо задать только один параметр. Например, для механической системы этим параметром является координата Связанные колебательные системы представляют собой системы с двумя и более степенями свободы, рассматриваемые как совокупность систем с одной степенью свободы, взаимодействующих между собой. Колебания, возникающие в связанных системах, называют связанными колебаниями. В дискретных связанных системах, состоящих из Примером связанных систем могут служить два колебательных контура, связанных между собой индуктивной связью (рис. 5.27, а). Колебания в одном контуре из-за наличия связи вызывают колебания в другом, т.е. происходит переход энергии из одного контура в другой. Число нормальных колебаний для таких контуров равно двум.
В линейных распределенных системах (струна, мембрана, резонатор) существует бесконечное, но счетное множество нормальных колебаний. Произвольное свободное колебание системы может быть представлено в виде суперпозиции нормальных колебаний. При этом полная энергия движения распадается на сумму энергий отдельных нормальных колебаний. Примером такой системы являются колебания струны, закрепленной на концах. Возбуждение в ней поперечных колебаний приводит к образованию стоячей волны, узлы которой приходятся на закрепленные концы (рис. 5.27, в). На длине струны
Все частоты
где F – сила натяжения струны; ρ, S – плотность материала струны и площадь ее поперечного сечения соответственно. Любое колебание струны можно представить в виде суммы ее нормальных колебаний. Таким образом, линейная распределенная система ведет себя как набор независимых гармонических осцилляторов. Полученная формула (5.92) используется, в частности, для определения спектра частот нормальных колебаний кристаллической решетки, связанных с тепловыми колебаниями атомов. Резонанс в системах с несколькими степенями свободы. При внешнем возбуждении системы нормальные колебания в значительной мере определяют ее резонансные свойства. Резонанс может возникнуть лишь в том случае, когда частота гармонического внешнего воздействия близка к одной из собственных частот системы, либо к их линейной комбинации, если внешнее воздействие меняет параметры системы (параметрический резонанс). В линейном приближении собственные колебания этих систем представляют собой набор нормальных колебаний (мод). Если отклик системы представляет собой суммарный отклик всех степеней свободы, то тогда резонансная кривая будет наложением резонансных кривых отдельных нормальных колебаний и может иметь сложный характер. Так, в системе с двумя степенями свободы, ввиду того, что собственные колебания могут происходить с двумя различными частотами, резонанс наступает при совпадении частоты гармонического внешнего воздействия как с одной, так и с другой нормальной частотой системы. Подбором параметров нормальных колебаний можно создать резонансную кривую любой формы, что широко используется, например, в радиотехнике для создания фильтрации частот (рис. 5.27, б). Наличие связи изменяет характер резонансных явлений в связанных системах по сравнению с одиночным контуром. В связанных системах резонанс наступает всякий раз, когда частота внешнего воздействия совпадает с одной из частот собственных колебаний всей системы, отличающихся от собственных частот отдельных контуров. Например, в связанных системах, состоящих из двух контуров, резонанс наступает на двух резонансных частотах. При этом для двух слабо взаимодействующих систем с близкими собственными частотами колебаний может происходить резонансная перекачка энергии из одной подсистемы в другую.
|

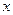 , описывающая движение материальной точки относительно положения равновесия (другие координаты у и z в этом случае не нужны). Для колебательного контура таким параметром будет заряд q на обкладках конденсатора (другие величины, такие как сила тока, напряжения на конденсаторе и на катушке, определяются из зависимости заряда q от времени t). Для линейных систем с одной степенью свободы существует только одно нормальное колебание, нормальная мода.
, описывающая движение материальной точки относительно положения равновесия (другие координаты у и z в этом случае не нужны). Для колебательного контура таким параметром будет заряд q на обкладках конденсатора (другие величины, такие как сила тока, напряжения на конденсаторе и на катушке, определяются из зависимости заряда q от времени t). Для линейных систем с одной степенью свободы существует только одно нормальное колебание, нормальная мода.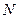 связанных гармонических осцилляторов (например, механических маятников, колебательных контуров), число нормальных колебаний равно
связанных гармонических осцилляторов (например, механических маятников, колебательных контуров), число нормальных колебаний равно 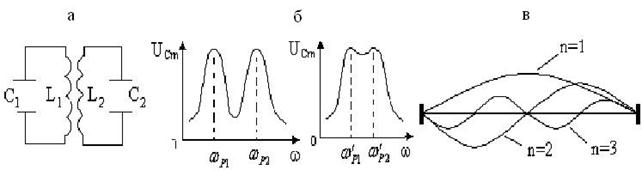 Рис. 5.27
Рис. 5.27 укладывается целое число полуволн
укладывается целое число полуволн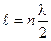 ,
, 
 , n= 1, 2, 3, …. (5.92)
, n= 1, 2, 3, …. (5.92) представляют собой частоты нормальных колебаний струны, частота
представляют собой частоты нормальных колебаний струны, частота 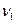 , соответствующая n= 1, называется основной частотой. Основную частоту можно изменить, уменьшая или увеличивая натяжение струны
, соответствующая n= 1, называется основной частотой. Основную частоту можно изменить, уменьшая или увеличивая натяжение струны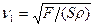 , (5.93)
, (5.93)


