Перепишем формулы (5.64) для I и  в удобном виде
в удобном виде
 ,
, 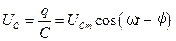 ,
,
и добавим к ним формулы для UL и UR:
 ,
,  .(5.77)
.(5.77)
Найдем в соответствии с полученными формулами разность фаз колебаний между силой тока 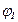 и напряжениями на конденсаторе
и напряжениями на конденсаторе  , индуктивности
, индуктивности  и активного сопротивления
и активного сопротивления  :
:
 , (5.78)
, (5.78)
 , (5.79)
, (5.79)
 . (5.80)
. (5.80)
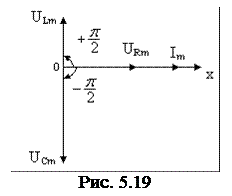 Как следует из формул (5.78) – (5.80) фаза колебаний напряжения на конденсаторе отстает по фазе от колебаний тока в цепи на π /2, а фаза колебаний напряжения на катушке опережает фазу колебаний силы тока на π /2. Фазы колебаний напряжения на активном сопротивлении R и силы тока в цепи совпадают. Это наглядно видно на векторной диаграмме, приведенной на рис. 5.19.
Как следует из формул (5.78) – (5.80) фаза колебаний напряжения на конденсаторе отстает по фазе от колебаний тока в цепи на π /2, а фаза колебаний напряжения на катушке опережает фазу колебаний силы тока на π /2. Фазы колебаний напряжения на активном сопротивлении R и силы тока в цепи совпадают. Это наглядно видно на векторной диаграмме, приведенной на рис. 5.19.
На ней указаны амплитуды векторов напряжений на отдельных участках электрической цепи. При этом фаза колебания силы тока в контуре принимается равной нулю, т.е. амплитуда вектора силы тока располагается вдоль оси 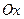 .
.
На такой диаграмме вектор амплитуды внешнего напряжения  , подаваемого в колебательный контур, можно представить как сумму векторов амплитуд напряжений (
, подаваемого в колебательный контур, можно представить как сумму векторов амплитуд напряжений ( ,
,  ,
, 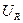 ) на разных его участках. Это позволяет записать следующую формулу для модуля вектора амплитуды внешнего напряжения (например, для частот
) на разных его участках. Это позволяет записать следующую формулу для модуля вектора амплитуды внешнего напряжения (например, для частот  , рис. 5.20, а):
, рис. 5.20, а):
 , (5.81)
, (5.81)
из которой с учетом формул (5.19) и (5.20) ( ) можно получить выражение (5.65) для зависимости амплитуды колебания заряда от частоты внешнего напряжения
) можно получить выражение (5.65) для зависимости амплитуды колебания заряда от частоты внешнего напряжения


 .
.

Рис. 5.20
Под фазовыми резонансными кривыми понимают, например, зависимости разности фаз 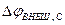 между внешним напряжением
между внешним напряжением  и напряжением
и напряжением  на конденсаторе, разности фаз
на конденсаторе, разности фаз  между внешним напряжением
между внешним напряжением  и силой тока I в контуре от частоты
и силой тока I в контуре от частоты  внешнего напряжения. Наиболее интересными из них являются зависимости
внешнего напряжения. Наиболее интересными из них являются зависимости 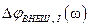 , так как они позволяют выяснить эффективность поступления энергии в контур (колебательную систему). В соответствии с формулами (5.64) и (5.66) для разности фаз
, так как они позволяют выяснить эффективность поступления энергии в контур (колебательную систему). В соответствии с формулами (5.64) и (5.66) для разности фаз 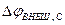 и
и  можно записать
можно записать
 ,
,  . (5.82)
. (5.82)
Отметим, что разность фаз  для цепей переменного тока обозначают буквой
для цепей переменного тока обозначают буквой  :
:  .
.
На рис. 5.21 приведены фазовые резонансные кривые  и
и  , построенные по формулам (5.66) и (5.82) при значениях параметра
, построенные по формулам (5.66) и (5.82) при значениях параметра  :
:  .
.

Рис. 5.21
Из них следует, что внешнее напряжение опережает по фазе напряжение на конденсаторе на угол  . На векторной диаграмме это означает, что вектор амплитуды
. На векторной диаграмме это означает, что вектор амплитуды  располагается выше вектора амплитуды
располагается выше вектора амплитуды  (рис. 5.20 а, б, в). Причем угол
(рис. 5.20 а, б, в). Причем угол  изменяется от нулевого значения для частоты
изменяется от нулевого значения для частоты  , равной нулю (
, равной нулю ( ), до значения равного
), до значения равного  при частоте внешнего напряжения стремящегося к бесконечности (
при частоте внешнего напряжения стремящегося к бесконечности ( , рис. 5.21, а). При резонансе амплитуды векторов внешнего напряжения
, рис. 5.21, а). При резонансе амплитуды векторов внешнего напряжения  и напряжения на конденсаторе
и напряжения на конденсаторе  взаимно перпендикулярны (см. рис. 5.20, б), что приводит к разности фаз между ними, равной
взаимно перпендикулярны (см. рис. 5.20, б), что приводит к разности фаз между ними, равной  (
( , Рис. 5.21, а).
, Рис. 5.21, а).
Из другой фазовой резонансной кривой следует, что фаза внешнего напряжения для частот 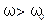 отстает от фазы тока в контуре на угол
отстает от фазы тока в контуре на угол  (рис.5.21, б). Для частот
(рис.5.21, б). Для частот 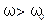 фаза внешнего напряжения опережает на угол
фаза внешнего напряжения опережает на угол  фазу колебаний силы тока в контуре и при увеличении частоты
фазу колебаний силы тока в контуре и при увеличении частоты  стремится к значению, равному
стремится к значению, равному  .При резонансе (
.При резонансе (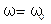 ,.
,. 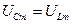 ) фаза колебаний силы тока и внешнего напряжения совпадают, т.е.
) фаза колебаний силы тока и внешнего напряжения совпадают, т.е. 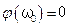 и вектора амплитуд
и вектора амплитуд  и
и  направлены одинаково, вдоль оси
направлены одинаково, вдоль оси 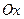 (рис. 5.21, б).
(рис. 5.21, б).
При этом энергия поступает в контур согласованно с колебаниями в ней. Действительно, учитывая выполнение условий малого затухания (Q > > 1) и формулы (5.64) и (5.66) запишем
 :
: 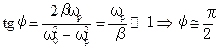 ;
;
 ,
, 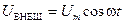 .
.
Такое поступление энергии в контур при резонансе приводит к большим амплитудам колебаний, их числовые значения определяются диссипацией (рассеянием) энергии системы, т. е. коэффициентом затухания  (формула (5.70)).
(формула (5.70)).
При частотах 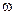 , больших или меньших
, больших или меньших 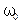 (
( ) амплитуда вынужденных колебаний даже в отсутствии диссипации энергии (
) амплитуда вынужденных колебаний даже в отсутствии диссипации энергии ( ) будет уменьшаться, она определяется расстройкой резонанса (
) будет уменьшаться, она определяется расстройкой резонанса ( ), т.е. разностью частот
), т.е. разностью частот 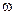 и
и 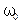 .
.
Можно отметить, что с использованием таблицы аналогий можно построить фазовые резонансные кривые для разности фаз между скоростью колебаний тела и действующей на него внешней силой в случае механической системы и т.д.

 в удобном виде
в удобном виде ,
, 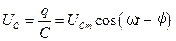 ,
, ,
,  .(5.77)
.(5.77)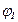 и напряжениями на конденсаторе
и напряжениями на конденсаторе  , индуктивности
, индуктивности  и активного сопротивления
и активного сопротивления  :
: , (5.78)
, (5.78) , (5.79)
, (5.79) . (5.80)
. (5.80) Как следует из формул (5.78) – (5.80) фаза колебаний напряжения на конденсаторе отстает по фазе от колебаний тока в цепи на π /2, а фаза колебаний напряжения на катушке опережает фазу колебаний силы тока на π /2. Фазы колебаний напряжения на активном сопротивлении R и силы тока в цепи совпадают. Это наглядно видно на векторной диаграмме, приведенной на рис. 5.19.
Как следует из формул (5.78) – (5.80) фаза колебаний напряжения на конденсаторе отстает по фазе от колебаний тока в цепи на π /2, а фаза колебаний напряжения на катушке опережает фазу колебаний силы тока на π /2. Фазы колебаний напряжения на активном сопротивлении R и силы тока в цепи совпадают. Это наглядно видно на векторной диаграмме, приведенной на рис. 5.19.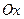 .
. , подаваемого в колебательный контур, можно представить как сумму векторов амплитуд напряжений (
, подаваемого в колебательный контур, можно представить как сумму векторов амплитуд напряжений ( ,
, 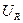 ) на разных его участках. Это позволяет записать следующую формулу для модуля вектора амплитуды внешнего напряжения (например, для частот
) на разных его участках. Это позволяет записать следующую формулу для модуля вектора амплитуды внешнего напряжения (например, для частот  , рис. 5.20, а):
, рис. 5.20, а): , (5.81)
, (5.81) ) можно получить выражение (5.65) для зависимости амплитуды колебания заряда от частоты внешнего напряжения
) можно получить выражение (5.65) для зависимости амплитуды колебания заряда от частоты внешнего напряжения

 .
.
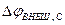 между внешним напряжением
между внешним напряжением  и напряжением
и напряжением  между внешним напряжением
между внешним напряжением  и силой тока I в контуре от частоты
и силой тока I в контуре от частоты  внешнего напряжения. Наиболее интересными из них являются зависимости
внешнего напряжения. Наиболее интересными из них являются зависимости 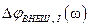 , так как они позволяют выяснить эффективность поступления энергии в контур (колебательную систему). В соответствии с формулами (5.64) и (5.66) для разности фаз
, так как они позволяют выяснить эффективность поступления энергии в контур (колебательную систему). В соответствии с формулами (5.64) и (5.66) для разности фаз  ,
,  . (5.82)
. (5.82) :
:  .
. и
и  , построенные по формулам (5.66) и (5.82) при значениях параметра
, построенные по формулам (5.66) и (5.82) при значениях параметра  :
:  .
.
 . На векторной диаграмме это означает, что вектор амплитуды
. На векторной диаграмме это означает, что вектор амплитуды  (рис. 5.20 а, б, в). Причем угол
(рис. 5.20 а, б, в). Причем угол  изменяется от нулевого значения для частоты
изменяется от нулевого значения для частоты  ), до значения равного
), до значения равного  при частоте внешнего напряжения стремящегося к бесконечности (
при частоте внешнего напряжения стремящегося к бесконечности ( , рис. 5.21, а). При резонансе амплитуды векторов внешнего напряжения
, рис. 5.21, а). При резонансе амплитуды векторов внешнего напряжения  взаимно перпендикулярны (см. рис. 5.20, б), что приводит к разности фаз между ними, равной
взаимно перпендикулярны (см. рис. 5.20, б), что приводит к разности фаз между ними, равной  (
( , Рис. 5.21, а).
, Рис. 5.21, а).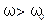 отстает от фазы тока в контуре на угол
отстает от фазы тока в контуре на угол  стремится к значению, равному
стремится к значению, равному  .При резонансе (
.При резонансе (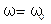 ,.
,. 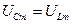 ) фаза колебаний силы тока и внешнего напряжения совпадают, т.е.
) фаза колебаний силы тока и внешнего напряжения совпадают, т.е. 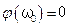 и вектора амплитуд
и вектора амплитуд  направлены одинаково, вдоль оси
направлены одинаково, вдоль оси  :
: 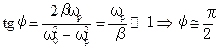 ;
; ,
, 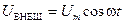 .
. (формула (5.70)).
(формула (5.70)).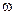 , больших или меньших
, больших или меньших 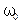 (
( ) амплитуда вынужденных колебаний даже в отсутствии диссипации энергии (
) амплитуда вынужденных колебаний даже в отсутствии диссипации энергии ( ) будет уменьшаться, она определяется расстройкой резонанса (
) будет уменьшаться, она определяется расстройкой резонанса ( ), т.е. разностью частот
), т.е. разностью частот 


