Уравнения вынужденных колебаний, их решения
Под вынужденными колебаниями понимают колебания, происходящие в системе в результате внешнего воздействия (внешней силы или внешнего напряжения), изменяющегося со временем по гармоническому закону. При этом колебания в системе происходят на циклической частоте Рассмотрим дифференциальное уравнение и его решение для вынужденных колебаний, происходящих в колебательном контуре под действием внешнего напряжения, изменяющегося по гармоническому закону
В этом случае дифференциальное уравнение (5.1) примет следующий вид:
Известно, что решением этого уравнения является следующее выражение
Из формулы (5.62) следует, что первое слагаемое представляет собой уравнение свободных затухающих колебаний системы и амплитуда этих колебаний с течением времени уменьшается. Если взять время t, большее времени установления стационарного режима колебаний в контуре (t > t уст), то тогда в выражении (5.62) останется только второе слагаемое (первым слагаемым можно пренебречь), которое представляет собой уравнение вынужденных колебаний заряда q на обкладках конденсатора t > t уст: Аналогичные уравнения можно записать для напряжения UC на конденсаторе и силы тока I в контуре
Как уже отмечалось, амплитуды колебаний этих величин зависят от частоты Выведем формулы для этих зависимостей. Для этого используем формулу Эйлера (5.40) для комплексной формы записи гармонического колебания.
Подставим эти выражения в формулу (5.61):
Два комплексных числа равны, если будут равны их вещественные и мнимые части, поэтому
Возведем каждое уравнение (5.64а) в квадрат, сложим их и получим
Разделим уравнения (5.64а) одно на другое, что приводит к формуле
Используя выражение (5.65), запишем
Рассмотрим подробнее резонансные кривые для амплитуды напряжения на конденсаторе
|

 внешнего воздействия, а амплитуды колебаний различных величин в системе будут зависеть от этой частоты.
внешнего воздействия, а амплитуды колебаний различных величин в системе будут зависеть от этой частоты.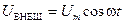 . (5.60)
. (5.60)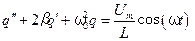 . (5.61)
. (5.61)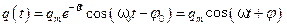 . (5.62)
. (5.62)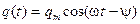 . (5.63)
. (5.63)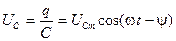 ,
,  . (5.64)
. (5.64) внешнего напряжения, такие зависимости называют резонансными кривыми:
внешнего напряжения, такие зависимости называют резонансными кривыми: 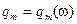 ,
,  ,
,  .
.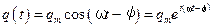 ,
, 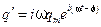 ,
, 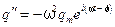 ,
, .
.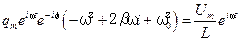 ,
, .
.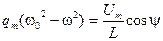 ,
, 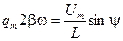 . (5.64а)
. (5.64а)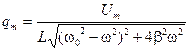 . (5.65)
. (5.65) . (5.66)
. (5.66)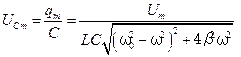 . (5.67)
. (5.67)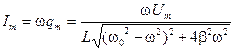 . (5.68)
. (5.68)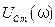 и амплитуды силы тока
и амплитуды силы тока  в контуре.
в контуре.


