Дифференциальное уравнение затухающих колебаний, его решение
Затухающие колебания происходят в замкнутой механической системе ( В этом случае общее дифференциальное уравнение колебаний (5.1) примет вид
Решением уравнения (5.44) являются затухающие колебания
где амплитуда колебаний
а циклическая частота затухающих колебаний
из которой следует, что
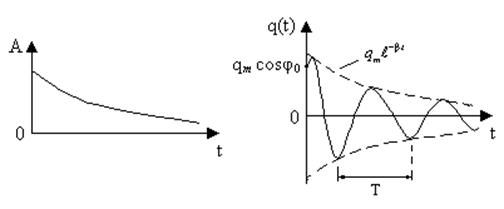
Графики зависимости от времени t амплитуды 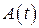 и заряда и заряда 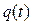 на обкладках конденсатора приведены на рис. 5.15. на обкладках конденсатора приведены на рис. 5.15.
Рис. 5.15
В случае механической системы по табл. аналогий 5.1 можно получить уравнения, подобные уравнениям (5.44), (5.45):
Отметим только, что для получения затухающих колебаний вида (5.49) необходимо, чтобы сила сопротивления, действующая в механической системе, была пропорциональна скорости движения тела
Только в этом случае получается дифференциальное уравнение затухающих колебаний в виде (5.48). Формула (5.50) справедлива для небольших числовых значений скоростей движения тела (м.т.). В заключение этого параграфа отметим, что из-за уменьшения с течением времени амплитуды колебаний затухающие колебания не являются периодическими. Но при малом затухании под периодом (его также называют условным периодом) можно понимать минимальное время, за которое повторяются минимальные значения или максимальные значения величин, описывающих колебательное движение (см. рис. 5.15). Аналогично циклическую частоту затухающих колебаний называют условной циклической частотой.
|

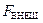 =0), в которой имеются потери энергии на преодоление сил сопротивления (β ≠ 0) или в закрытом колебательном контуре (U внеш=0), в котором наличие сопротивления R приводит к потерям энергии колебаний на нагревание проводников (β ≠ 0).
=0), в которой имеются потери энергии на преодоление сил сопротивления (β ≠ 0) или в закрытом колебательном контуре (U внеш=0), в котором наличие сопротивления R приводит к потерям энергии колебаний на нагревание проводников (β ≠ 0).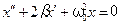 . (5.44)
. (5.44)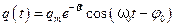 , (5.45)
, (5.45)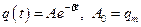 (5.46)
(5.46)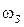 определяется формулой
определяется формулой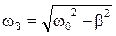 , (5.47)
, (5.47)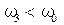 .
.
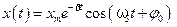 . (5.49)
. (5.49)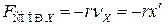 . (5.50)
. (5.50)


