Возьмем ось 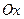 . Из начала оси (точка О) отложим вектор
. Из начала оси (точка О) отложим вектор 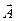 под углом
под углом  к оси
к оси 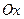 (рис. 5.6). Если этот вектор вращать вокруг точки
(рис. 5.6). Если этот вектор вращать вокруг точки  с угловой скоростью
с угловой скоростью 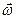 , то тогда проекция вектора
, то тогда проекция вектора 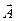 на ось
на ось 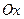 будет изменяться по гармоническому закону
будет изменяться по гармоническому закону
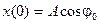 ,
, 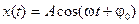 .
.
Такое построение называют векторной диаграммой. Гармоническое колебание на векторной диаграмме совершает проекция вектора 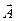 на ось
на ось 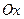 . Причем циклическая частота
. Причем циклическая частота  колебаний будет равна по модулю угловой скорости
колебаний будет равна по модулю угловой скорости 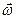 вращения вектора
вращения вектора 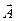 .
.
 Пусть тело (м.т.) одновременно участвует в двух гармонических колебаниях одинаковой частоты, происходящих в одном направлении, причем амплитуды и начальные фазы колебаний различны (
Пусть тело (м.т.) одновременно участвует в двух гармонических колебаниях одинаковой частоты, происходящих в одном направлении, причем амплитуды и начальные фазы колебаний различны (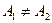 ,
, 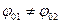 ):
):
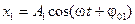 ,
, 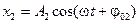 . (5.24)
. (5.24)
Результирующее движение, равное сумме колебаний 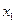 и
и 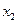 , будет также гармоническим колебанием той же циклической частоты
, будет также гармоническим колебанием той же циклической частоты 
Рис. 5.6
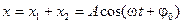 .
.
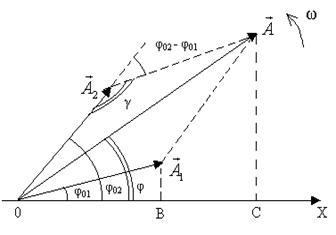
Необходимо найти амплитуду и начальную фазу результирующего колебания. Это можно сделать с помощью векторной диаграммы. Для этого проведем из точки О векторы с амплитудами А1 и А2 под углами  и
и 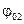 к оси
к оси 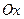 и приведем их во вращение с угловой скоростью
и приведем их во вращение с угловой скоростью 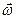 (рис. 5.7).
(рис. 5.7).
Проекции векторов  и
и 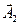 на ось
на ось 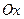 при этом совершают гармонические колебания в соответствии с уравнениями (5.24). Результирующее колебание будет изображаться проекцией на ось
при этом совершают гармонические колебания в соответствии с уравнениями (5.24). Результирующее колебание будет изображаться проекцией на ось 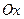 вектора
вектора 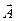 , полученного из векторов
, полученного из векторов 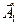 и
и 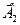 по правилу параллелограмма. Из построения на Рис. 5.7 следует, что квадрат амплитуды вектора
по правилу параллелограмма. Из построения на Рис. 5.7 следует, что квадрат амплитуды вектора 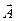 можно найти по теореме косинусов из треугольника Δ ОА2А:
можно найти по теореме косинусов из треугольника Δ ОА2А:
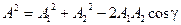 ,
, 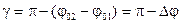
 . (5.25)
. (5.25)
Из треугольников Δ ОА1В и Δ ОАС для начальной фазы  результирующего колебания можно найти следующее выражение:
результирующего колебания можно найти следующее выражение:
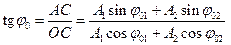 . (5.26)
. (5.26)
Рассмотрим частные случаи сложения колебаний.
1. 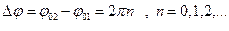
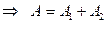 , (5.27)
, (5.27)
т.е. если разность фаз складываемых колебаний равна четному числу π, то колебания максимально усиливают друг друга.
2. 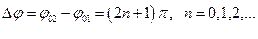
 , (5.28)
, (5.28)
 т.е., если разность фаз складываемых колебаний равна нечетному числу π, то колебания максимально ослабляют друг друга.
т.е., если разность фаз складываемых колебаний равна нечетному числу π, то колебания максимально ослабляют друг друга.
3. 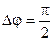
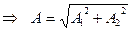 .
.
На рис. 5.8 приведены результаты сложения гармонических колебаний в рассмотренных выше случаях 1, 2 и 3, при условии, что  =0 и А 1> А 2.
=0 и А 1> А 2.
Рис. 5.7
Полученные условия максимального усиления (5.27) и ослабления (5.28) колебаний при сложении колебаний одного направления и одинаковой частоты
будут использованы при изучении интерференции когерентных волн.

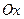 . Из начала оси (точка О) отложим вектор
. Из начала оси (точка О) отложим вектор 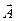 под углом
под углом  к оси
к оси  с угловой скоростью
с угловой скоростью  , то тогда проекция вектора
, то тогда проекция вектора 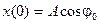 ,
, 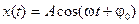 .
. колебаний будет равна по модулю угловой скорости
колебаний будет равна по модулю угловой скорости  Пусть тело (м.т.) одновременно участвует в двух гармонических колебаниях одинаковой частоты, происходящих в одном направлении, причем амплитуды и начальные фазы колебаний различны (
Пусть тело (м.т.) одновременно участвует в двух гармонических колебаниях одинаковой частоты, происходящих в одном направлении, причем амплитуды и начальные фазы колебаний различны (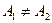 ,
, 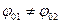 ):
):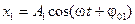 ,
, 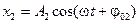 . (5.24)
. (5.24) и
и  , будет также гармоническим колебанием той же циклической частоты
, будет также гармоническим колебанием той же циклической частоты 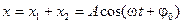 .
. и
и 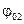 к оси
к оси  и
и 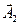 на ось
на ось 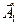 и
и 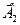 по правилу параллелограмма. Из построения на Рис. 5.7 следует, что квадрат амплитуды вектора
по правилу параллелограмма. Из построения на Рис. 5.7 следует, что квадрат амплитуды вектора 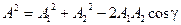 ,
, 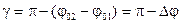
 . (5.25)
. (5.25)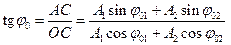 . (5.26)
. (5.26)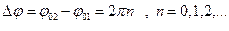
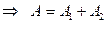 , (5.27)
, (5.27)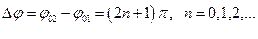
 , (5.28)
, (5.28) т.е., если разность фаз складываемых колебаний равна нечетному числу π, то колебания максимально ослабляют друг друга.
т.е., если разность фаз складываемых колебаний равна нечетному числу π, то колебания максимально ослабляют друг друга.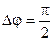
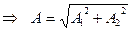 .
.


