Сложение N гармонических колебаний одного направления, одинаковой амплитуды и частоты, начальные фазы которых образуют арифметическую прогрессию
Рассмотрим сложение N гармонических колебаний, происходящих вдоль оcи
что позволяет написать
Полученная формула будет использована при расчете результата многолучевой интерференции на дифракционной решетке. Биения
Биения – это колебания, которые получаются в результате сложения двух гармонических колебаний х1 и х2 одного направления с близкими частотами (
Рассмотрим подробнее результат сложения таких колебаний. Для простоты расчетов будем считать, что амплитуды складываемых колебаний одинаковы:
запишем
Первый сомножитель в выражении (5.30) изменяется со временем значительно медленнее второго (
Итак, биения можно представить как колебания с периодически изменяющейся амплитудой. Эти колебания не являются гармоническими колебаниями. В общем случае амплитуда биений изменяется в пределах, заключенных от
На рис. 5.10 приведены графики зависимости амплитуды биений
Рис. 5.10
Метод биений применяют, например, для настройки музыкальных инструментов, при анализе восприятия звуков человеком. Наглядно биения можно продемонстрировать на опыте, в котором звуковой генератор возбуждает два колебания разной частоты, которые человеческое ухо различает как два отдельных звуковых сигнала. Если сближать частоты этих сигналов, то при некоторой разности частот (она зависит от слухового восприятия конкретного человека) вместо двух сигналов ухо человека будет воспринимать звуковой сигнал одной частоты, амплитуда которого будет изменяться, т.е. в этом случае наблюдаются биения. При дальнейшем сближении частот период биений будет увеличиваться и при совпадении частот сигналов будет слышен звук одной частоты, амплитуда которого не будет изменяться. Биения можно использовать, например, для определения частоты какого-либо гармонического электрического колебания. Для этого на вход осциллографа подают гармонические колебания от звукового генератора (частоту
|

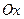
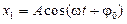 ,
, 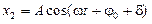 ,
,  , …,
, …,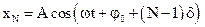 .
.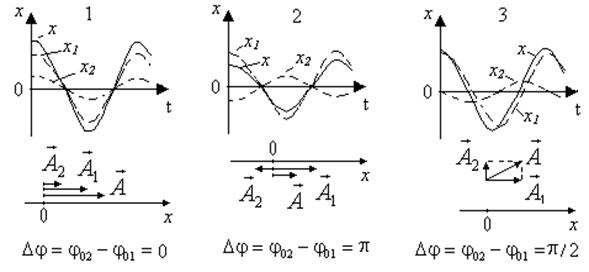 Рис. 5.8
Рис. 5.8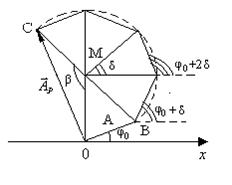 Найдем с помощью векторной диаграммы амплитуду АР результирующего колебания (рис. 5.9). Для этого отложим вектор первого колебания амплитуды А из точки О, он будет составлять угол φ 0 с осью Ох; вектор второго колебания будем откладывать из конца первого вектора, угол между вторым вектором и осью Ох будет равен (φ 0+δ) и т.д. В результате получается ломаная линия, вписанная в окружность радиуса R. Вектор результирующего колебания замыкает эту ломаную линию и определяется следующим образом
Найдем с помощью векторной диаграммы амплитуду АР результирующего колебания (рис. 5.9). Для этого отложим вектор первого колебания амплитуды А из точки О, он будет составлять угол φ 0 с осью Ох; вектор второго колебания будем откладывать из конца первого вектора, угол между вторым вектором и осью Ох будет равен (φ 0+δ) и т.д. В результате получается ломаная линия, вписанная в окружность радиуса R. Вектор результирующего колебания замыкает эту ломаную линию и определяется следующим образом
 ,
,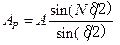 . (5.29)
. (5.29) > >
> > 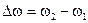 )/
)/ ,
,  ,
,  .
. . Тогда используя известную формулу сложения косинусов
. Тогда используя известную формулу сложения косинусов ,
,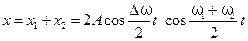 . (5.30)
. (5.30)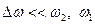 ) и поэтому можно считать, что результирующее колебание
) и поэтому можно считать, что результирующее колебание 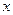 представляет собой колебание с циклической частотой
представляет собой колебание с циклической частотой 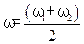 и с изменяющейся со временем амплитудой
и с изменяющейся со временем амплитудой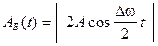 . (5.31)
. (5.31) до (
до ( ). При этом период изменения амплитуды (период биений
). При этом период изменения амплитуды (период биений 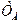 ) и циклическая частота
) и циклическая частота 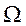 биений будут определяться по формулам
биений будут определяться по формулам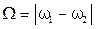 ,
, 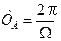 . (5.32)
. (5.32) и смещения
и смещения 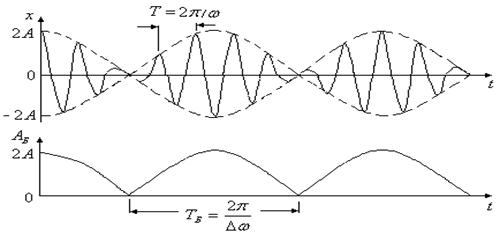
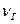 этих колебаний можно изменять) и гармонические колебания с неизвестной частотой
этих колебаний можно изменять) и гармонические колебания с неизвестной частотой 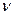 от какого-либо источника. По наблюдаемой на экране осциллографа картине биений определяют период биений
от какого-либо источника. По наблюдаемой на экране осциллографа картине биений определяют период биений 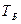 и частоту колебаний (
и частоту колебаний (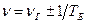 ). Знак плюс или минус в записанной формуле определяется следующим образом: если при увеличении частоты
). Знак плюс или минус в записанной формуле определяется следующим образом: если при увеличении частоты 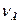 генератора период биений, наблюдаемых на экране, увеличивается, то тогда в формуле выбирается знак плюс (
генератора период биений, наблюдаемых на экране, увеличивается, то тогда в формуле выбирается знак плюс (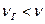 ), в противном случае – знак минус (
), в противном случае – знак минус (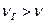 ).
).



