Механические незатухающие гармонические колебания в замкнутой системе
Для замкнутой системы (
Из теории дифференциальных уравнений следует, что решением этого уравнения(его называют однородным линейным дифференциальным уравнением второго порядка) является гармоническое колебание
т.е. смещение х тела (материальной точки) от положения равновесия изменяется по гармоническому закону. В уравнении (5.7) введены такие понятия, как хm – максимальное смещение или амплитуда колебания. В общем случае под амплитудой колебаний понимают положительную величину, стоящую перед знаком синуса или косинуса;
Циклическая частота
Запишем выражения для проекций скорости, проекции ускорения тела (м.т.) на ось Ох, потенциальной, кинетической и полной энергий тела, совершающего гармонические колебания
Покажем, что амплитуды колебаний кинетической и потенциальной энергий совпадают
Тогда
Итак, из полученных формул следует, что проекция скорости Приведем в пределах одного периода Т колебаний графики зависимости х,
Рис. 5.4
Отметим, что для потенциальной и кинетической энергий период гармонических колебаний оказывается в два раза меньше, чем для смещения х.
|

 =0), в которой отсутствуют потери энергии на преодоление сил сопротивления или трения (β =0), дифференциальное уравнение (5.4) примет вид
=0), в которой отсутствуют потери энергии на преодоление сил сопротивления или трения (β =0), дифференциальное уравнение (5.4) примет вид . (5.6)
. (5.6) , (5.7)
, (5.7) -– фаза колебаний – величина, стоящая под знаком синуса или косинуса;
-– фаза колебаний – величина, стоящая под знаком синуса или косинуса; – начальная фаза колебаний – фаза колебаний в начальный момент времени t =0;
– начальная фаза колебаний – фаза колебаний в начальный момент времени t =0; – циклическая (круговая) частота свободных незатухающих гармонических колебаний системы, определяемая свойствами системы по формуле (5.5).
– циклическая (круговая) частота свободных незатухающих гармонических колебаний системы, определяемая свойствами системы по формуле (5.5). . (5.8)
. (5.8) ,
,  ; (5.9)
; (5.9) ,
,  ,
,  ; (5.10)
; (5.10) ,
,  ; (5.11)
; (5.11) ,
, 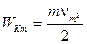 . (5.12)
. (5.12) .
. . (5.13)
. (5.13) и ускорения
и ускорения  , кинетическая и потенциальная энергии WK, WP тела (м.т.) изменяются по гармоническому закону подобно ее смещению х, а полная энергия W колебаний м.т. остается при этом неизменной.
, кинетическая и потенциальная энергии WK, WP тела (м.т.) изменяются по гармоническому закону подобно ее смещению х, а полная энергия W колебаний м.т. остается при этом неизменной. ). При построении графиков удобно записать уравнения колебаний в виде
). При построении графиков удобно записать уравнения колебаний в виде  и выбирать моменты времени, равные
и выбирать моменты времени, равные  Þ
Þ  .
.



