Квазиупругая сила. Математический и физический маятники. Гармонический осциллятор
Докажем следующее утверждение: если в системе результирующая сила является квазиупругой, то в такой системе происходят гармонические колебания. Под квазиупругой силой Докажем это утверждение. Учтем, что, для FКу выполняется одновременно и второй закон Ньютона и закон Гука, из которых можно получить дифференциальное уравнение колебаний в системе
где Как уже было отмечено выше, решением такого дифференциального уравнения является гармоническое колебание (5.7), что и требовалось доказать. В качестве примера справедливости этого утверждения рассмотрим колебания математического маятника - это материальная точка массы m, подвешенная на невесомой нерастяжимой нити длины l (рис. 5.5, а) Найдем проекцию на ось Ох результирующей силы, действующей на груз математического маятника. Учитывая малые значения угла отклонения
Итак, при малых отклонениях от положения равновесия (при малых амплитудах колебаний) колебания груза будут гармоническими. Это позволяет найти период колебаний
Как следует из формулы (5.14), период колебаний математического маятника будет зависеть от длины нити l и числового значения ускорения g свободного падения. Рассмотрим теперь общий случай - случай колебаний физического маятника. Физическим маятником называют твердое тело, способное под действием силы тяжести совершать колебания вокруг неподвижной горизонтальной оси (точка О, рис. 5.5, б). При этом ось вращения не проходит через центр тяжести (центр масс) тела (точка О', рис. 5.5, б). Расстояние между точками О и О' обозначено буквой а (ОО' = а).
Как уже было отмечено выше, решением полученного дифференциального уравнения является гармоническое колебание. Тогда для периода колебаний физического маятника можно записать следующую формулу:
где введена приведенная длина физического маятника Рассмотренные выше примеры (колебательный контур, математический и физический маятники, колебания груза на пружине) являются частными случаями движения гармонического осциллятора. Под осциллятором (от латинского слова oscillo -качаюсь) понимают любую физическую систему, совершающую колебания. Если колебания в системе будут гармоническими, то такой осциллятор называют гармоническим осциллятором. Для механических систем результирующая сила в этом случае является квазиупругой, а потенциальное поле, в котором движется тело, имеет параболический вид ( Если отклонение Понятие осциллятора применяется также и к немеханическим колебательным системам. В частности, колебательный контур является электрическим осциллятором.
|

 понимают силу, которая подчиняется закону Гука, но не является по своей природе упругой силой.
понимают силу, которая подчиняется закону Гука, но не является по своей природе упругой силой. , Þ
, Þ  ,
,  ,
, – коэффициент жесткости системы, х - смещение тела (м.т.) от положения равновесия.
– коэффициент жесткости системы, х - смещение тела (м.т.) от положения равновесия. (
( ) запишем
) запишем
 .
. . (5.14)
. (5.14) Покажем, что при малых углах отклонения
Покажем, что при малых углах отклонения  ) от положения равновесия (ему соответствует расположение точек О и О' на одной вертикальной прямой) колебания физического маятника будут гармоническими. Для этого запишем второй закон Ньютона для вращательного движения в векторном виде и в проекциях на ось вращения (см. раздел " Механика", формула (1.46))
) от положения равновесия (ему соответствует расположение точек О и О' на одной вертикальной прямой) колебания физического маятника будут гармоническими. Для этого запишем второй закон Ньютона для вращательного движения в векторном виде и в проекциях на ось вращения (см. раздел " Механика", формула (1.46)) ,
,  ,
, 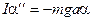 ,
, Þ
Þ  ,
,  . (5.15)
. (5.15) ,
,  . (5.16)
. (5.16) - это такая длина математического маятника, при которой периоды колебаний физического и математического маятников совпадают.
- это такая длина математического маятника, при которой периоды колебаний физического и математического маятников совпадают. ), что наблюдается при малых отклонениях х системы от положения равновесия.
), что наблюдается при малых отклонениях х системы от положения равновесия. нельзя считать малым, то тогда в разложении
нельзя считать малым, то тогда в разложении  по степеням
по степеням  ), уравнения движения становятся нелинейными, а сам осциллятор в этом случае называют ангармоническим осциллятором.
), уравнения движения становятся нелинейными, а сам осциллятор в этом случае называют ангармоническим осциллятором.


