 Выведем общее дифференциальное уравнение, описывающее достаточно широкий круг происходящих в системе колебаний. Для этого рассмотрим открытый колебательный контур, в который подается внешнее напряжение
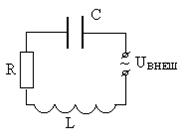
Выведем общее дифференциальное уравнение, описывающее достаточно широкий круг происходящих в системе колебаний. Для этого рассмотрим открытый колебательный контур, в который подается внешнее напряжение  и имеются потери энергии на нагревание проводников (рис. 5.3).
и имеются потери энергии на нагревание проводников (рис. 5.3).
Из закона сохранения энергии следует, что элементарная работа 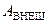 тока, поступающего в контур извне, расходуется на изменение энергии колебаний
тока, поступающего в контур извне, расходуется на изменение энергии колебаний  и на нагревание проводников
и на нагревание проводников  :
:
Рис. 5.3
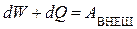 .
.
Распишем это выражение
 ,
,
 ,
,  ,
,
 ,
, 
 ,
,
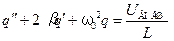 , (5.1)
, (5.1)
где введены следующие обозначения:
 , (5.2)
, (5.2)
 . (5.3)
. (5.3)
Буквой β в формуле (5.2) обозначен коэффициент затухания колебаний, а величина  в формуле (5.3) называется циклической (круговой) частотой свободных незатухающих гармонических колебаний контура. Свободные незатухающие колебания происходят в выведенной из состояния равновесия замкнутой системе (нет поступления энергии извне), в которой отсутствуют потери энергии колебаний (β =0).
в формуле (5.3) называется циклической (круговой) частотой свободных незатухающих гармонических колебаний контура. Свободные незатухающие колебания происходят в выведенной из состояния равновесия замкнутой системе (нет поступления энергии извне), в которой отсутствуют потери энергии колебаний (β =0).
Уравнение (5.1) описывает различные случаи колебаний в открытом и закрытом колебательных контурах. Для получения аналогичного уравнения, описывающего колебания в механической системе, воспользуемся табл. аналогий 5.1:
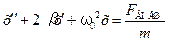 , (5.4)
, (5.4)
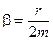 ,
,  , (5.5)
, (5.5)
где  – проекция вектора внешней силы на ось Ох, вдоль которой происходят колебания.
– проекция вектора внешней силы на ось Ох, вдоль которой происходят колебания.
Рассмотрим частные случаи решения уравнений (5.1) и (5.4).

 Выведем общее дифференциальное уравнение, описывающее достаточно широкий круг происходящих в системе колебаний. Для этого рассмотрим открытый колебательный контур, в который подается внешнее напряжение
Выведем общее дифференциальное уравнение, описывающее достаточно широкий круг происходящих в системе колебаний. Для этого рассмотрим открытый колебательный контур, в который подается внешнее напряжение  и имеются потери энергии на нагревание проводников (рис. 5.3).
и имеются потери энергии на нагревание проводников (рис. 5.3).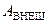 тока, поступающего в контур извне, расходуется на изменение энергии колебаний
тока, поступающего в контур извне, расходуется на изменение энергии колебаний  и на нагревание проводников
и на нагревание проводников  :
: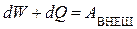 .
. ,
, ,
,  ,
, ,
, 
 ,
,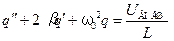 , (5.1)
, (5.1) , (5.2)
, (5.2) . (5.3)
. (5.3) в формуле (5.3) называется циклической (круговой) частотой свободных незатухающих гармонических колебаний контура. Свободные незатухающие колебания происходят в выведенной из состояния равновесия замкнутой системе (нет поступления энергии извне), в которой отсутствуют потери энергии колебаний (β =0).
в формуле (5.3) называется циклической (круговой) частотой свободных незатухающих гармонических колебаний контура. Свободные незатухающие колебания происходят в выведенной из состояния равновесия замкнутой системе (нет поступления энергии извне), в которой отсутствуют потери энергии колебаний (β =0).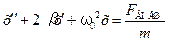 , (5.4)
, (5.4)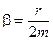 ,
,  , (5.5)
, (5.5) – проекция вектора внешней силы на ось Ох, вдоль которой происходят колебания.
– проекция вектора внешней силы на ось Ох, вдоль которой происходят колебания.


