Спектральное представление различных сигналов
Как известно, общий подход к анализу сложных процессов и явлений заключается в их разложении на более простые процессы и явления. Этот же подход может быть применен к анализу периодических процессов, учитывая, что наиболее простыми среди периодических функций являются гармонические колебания. Любое сложное колебание можно представить в виде суммы гармонических колебаний, их называют гармониками. Разложение сложного колебания на гармонические колебания (без учета их фаз) называется спектральным разложением. Диаграмма, изображающая зависимость амплитуды каждой гармоники от ее частоты, называется спектром сложного колебания или спектром амплитуд. В качестве примера приведем спектры амплитуд для различных периодических колебаний 1. Гармоническое колебание с частотой Спектр амплитуд для такой функции представляет собой одну линию амплитуды А на частоте 2. Биения (частный случай одинаковых амплитуд складываемых колебаний - Спектр амплитуд представляет собой две близко расположенные линии c амплитудами А и с частотами 3. Амплитудно-модулированное колебание: Как следует из формулы (5.36), спектр этого колебания представляет собой три линии с частотами
Рис. 5.14 4. Наиболее общий случай: произвольная периодическая функция В этом случае спектр амплитуд не будет таким простым, как в приведенных выше примерах. В математике доказывается, что при условиях, которые обычно выполняются в физических задачах, периодическую функцию
где коэффициенты Фурье Совокупность величин В качестве примера приведем спектр амплитуд пилообразной периодической функции
Можно показать, что коэффициенты Фурье в этом случае будут равны
Спектр амплитуд для такой периодической функции приведен на рис. 5.14, г. Он представляет собой бесконечный дискретный набор гармоник, амплитуды которых убывают обратно пропорционально номеру гармоники. 5. Функция
Величины
где Нужно помнить, что комплексная форма записи гармонических колебаний удобна при проведении расчетов или математических выкладок. При переходе от комплексной формы записи к реальной функции берут вещественную часть комплексного числа
В качестве примера непериодической функции
. Таким образом, периодические функции характеризуются дискретными спектрами амплитуд, а непериодические – непрерывными спектрами амплитуд. Ограниченные во времени непериодические функции представляют собой импульсные сигналы (их еще также называют импульсами), для которых можно ввести понятия продолжительности импульса Можно показать, что ширина
где за ширину В заключение параграфа отметим, что исследование спектрального состава временных процессов, представление их в виде набора самого простого вида колебаний – гармонических колебаний, имеют ряд неоспоримых преимуществ и поэтому широко применяются во многих разделах не только физики, но и других естественных наук. К таким преимуществам можно отнести, например, простую и наглядную классификацию временных процессов по спектру их амплитуд; методику анализа распространения различных сигналов в средах по изменению частотного спектра сигнала; целенаправленное изменение временных сигналов по изменению их частотного спектра и т.д.
|

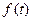 .
.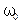 :
: 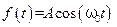 .
. ):
): 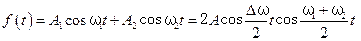 .
.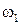 и
и  (рис. 5.14, б).
(рис. 5.14, б).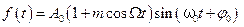 .
. ,
, 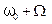 и с амплитудами
и с амплитудами 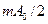 , А и
, А и 
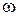 (
( ) изменения функции
) изменения функции 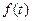 и принимают значения
и принимают значения 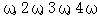 и т.д. Такая сумма называется рядом Фурье или гармоническим разложением сложного периодического колебания.
и т.д. Такая сумма называется рядом Фурье или гармоническим разложением сложного периодического колебания. , (5.37)
, (5.37)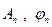 определяются видом функции
определяются видом функции  называется спектром амплитуд функции
называется спектром амплитуд функции 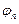 – спектром фаз. Слагаемое ряда Фурье с частотой
– спектром фаз. Слагаемое ряда Фурье с частотой  называют первой (основной) гармоникой, а остальные – высшими (второй, третьей и т.д.) гармониками или обертонами функции
называют первой (основной) гармоникой, а остальные – высшими (второй, третьей и т.д.) гармониками или обертонами функции 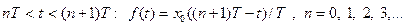 .
.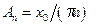 ,
, 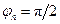
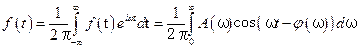 , (5.38)
, (5.38) ,
,  . (5.39)
. (5.39)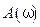 и
и 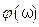 представляют амплитудный спектр и фазовый спектр функции
представляют амплитудный спектр и фазовый спектр функции 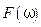 называют Фурье-образом функции
называют Фурье-образом функции  , (5.40)
, (5.40)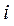 – мнимая единица:
– мнимая единица: 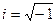 .
.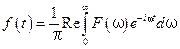 . (5.41)
. (5.41)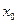 , ограниченный интервалом времени
, ограниченный интервалом времени 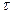 (рис. 5.14, д). Спектр амплитуд такого импульса является сплошным (рис. 5.14, е), причем
(рис. 5.14, д). Спектр амплитуд такого импульса является сплошным (рис. 5.14, е), причем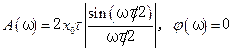 . (5.42)
. (5.42)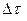 и ширины
и ширины  спектраимпульса. Продолжительность импульса
спектраимпульса. Продолжительность импульса 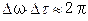 , (5.43)
, (5.43)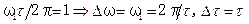 (см. рис.5.14, е). Равенство (5.43) часто используется для приближенной оценки ширины частотного спектра различных импульсов.
(см. рис.5.14, е). Равенство (5.43) часто используется для приближенной оценки ширины частотного спектра различных импульсов.


