Исследуем функцию 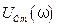 (5.67) для различных значений угловой частоты внешнего напряжения
(5.67) для различных значений угловой частоты внешнего напряжения  .
.
1.ω =0: 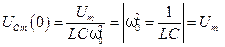 ,
,
т.е. постоянное напряжение, подаваемое в контур, представляет собой напряжение на конденсаторе или все резонансные кривые для частоты  , равной нулю (
, равной нулю (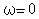 ), выходят из одной точки.
), выходят из одной точки.
2. 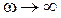 :
: 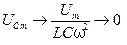 ,
,
т.е. при больших частотах внешнего воздействия все резонансные кривые стремятся к нулю. Это связано с тем, что система не успевает за изменениями внешнего воздействия и амплитуда колебаний в контуре уменьшается.
3.  . Найдем угловую частоту
. Найдем угловую частоту 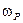 , при которой зависимость
, при которой зависимость  имеет максимальное значение. Оно будет наблюдаться в том случае, когда выражение под знаком квадратного корня в формуле (5.67) будет минимальным. Поэтому
имеет максимальное значение. Оно будет наблюдаться в том случае, когда выражение под знаком квадратного корня в формуле (5.67) будет минимальным. Поэтому
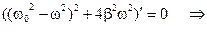
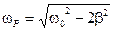 . (5.69)
. (5.69)
Подставляя 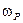 в формулу (5.67), для максимального значения амплитуды напряжения на конденсаторе получим
в формулу (5.67), для максимального значения амплитуды напряжения на конденсаторе получим
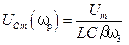 . (5.70)
. (5.70)
Величина 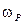 получила название резонансной частоты. В условиях малого затухания (Q > > 1) для частоты
получила название резонансной частоты. В условиях малого затухания (Q > > 1) для частоты  можно записать
можно записать
 , (5.71)
, (5.71)
т.е. амплитуда вынужденных колебаний напряжения на конденсаторе во много раз превышает амплитуду внешнего напряжения, подаваемого в контур. Это явление получило название явления резонанса. Под резонансом понимают явление резкого возрастания амплитуды вынужденных колебаний при приближении частоты внешнего воздействия к частоте собственных свободных незатухающих колебаний системы.
На рис. 5.17, а приведены резонансные кривые 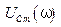 для идеального колебательного контура (
для идеального колебательного контура (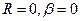 ) и для двух значений сопротивления R в нем (
) и для двух значений сопротивления R в нем (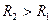 , т.е.
, т.е. 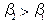 ). При этом считается, что индуктивность L катушки и электроемкость C конденсатора контура не изменяются, т.е. частота
). При этом считается, что индуктивность L катушки и электроемкость C конденсатора контура не изменяются, т.е. частота 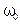 при этом остается неизменной.
при этом остается неизменной.
Можно отметить, что для идеального колебательного контура максимум резонансной кривой 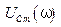 приходится на частоту
приходится на частоту 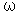 , равную
, равную 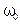 (
(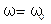 ), причем максимальное значение при этом стремится к бесконечности (рис.5.17, а). При увеличении сопротивления
), причем максимальное значение при этом стремится к бесконечности (рис.5.17, а). При увеличении сопротивления  контура коэффициент затухания
контура коэффициент затухания 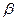 увеличивается, а максимальное значение
увеличивается, а максимальное значение 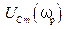 и частота
и частота 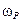 , на которую он приходится, уменьшаются (рис. 5.17, а).
, на которую он приходится, уменьшаются (рис. 5.17, а).
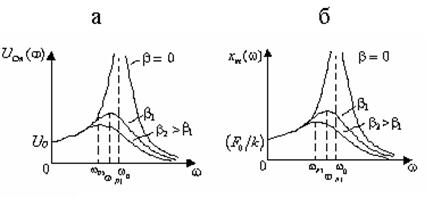
Рис. 5.17
В случае механической системы резонансную кривую  для амплитуды смещения груза (м.т.) от положения равновесия можно получить, используя табл. аналогий 5.1:
для амплитуды смещения груза (м.т.) от положения равновесия можно получить, используя табл. аналогий 5.1:
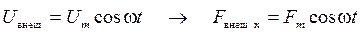 ;
;
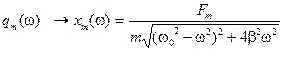 ;
; 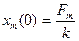 ;
; 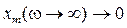 . (5.72)
. (5.72)
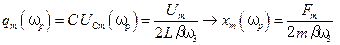 . (5.73)
. (5.73)
Графики резонансных зависимостей 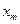 от
от 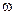 при различных значениях коэффициента затухания
при различных значениях коэффициента затухания 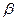 , т.е. при различных значениях коэффициента r сопротивления среды, и постоянной частоте
, т.е. при различных значениях коэффициента r сопротивления среды, и постоянной частоте  приведены на рис.5.17, б.
приведены на рис.5.17, б.
5.10.3. Резонансные кривые для амплитуды силы тока в контуре,
для амплитуды скорости материальной точки в механической системе
Запишем формулу (5.68) для амплитуды силы тока 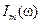 в наиболее удобном виде
в наиболее удобном виде
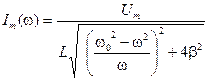 ,
,
и исследуем эту зависимость для различных значений 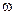 .
.
1.ω =0:  , т.е. постоянный электрический ток через цепь, содержащую конденсатор, не протекает.
, т.е. постоянный электрический ток через цепь, содержащую конденсатор, не протекает.
2. 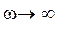 :
: 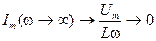 .
.
3. Максимум функции 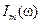 наблюдается тогда, когда подкоренное выражение в знаменателе будет минимальным, т.е. первое слагаемое в подкоренном выражении должно быть равным нулю. Поэтому максимум
наблюдается тогда, когда подкоренное выражение в знаменателе будет минимальным, т.е. первое слагаемое в подкоренном выражении должно быть равным нулю. Поэтому максимум 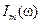 соответствует частоте
соответствует частоте 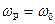 , а само максимальное значение будет равно
, а само максимальное значение будет равно
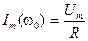 . (5.74)
. (5.74)
На рис. 5.18 приведены резонансные кривые 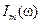 в случае идеального колебательного контура (
в случае идеального колебательного контура (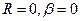 ) и для двух разных значений сопротивления
) и для двух разных значений сопротивления  в нем (
в нем (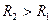 , т.е.
, т.е. 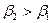 ) при постоянном значении
) при постоянном значении  . Как видно, максимум функции с увеличением
. Как видно, максимум функции с увеличением  уменьшается, а его смещение по оси частот
уменьшается, а его смещение по оси частот 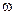 не происходит.
не происходит.
Используя табл. аналогий 5.1, можно записать формулы, описывающие резонансные кривые для амплитуды колебаний скорости 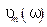 тела (м.т.) в механической системе:
тела (м.т.) в механической системе:
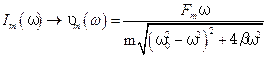 , (5.75)
, (5.75)
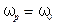 :
:  . (5.76)
. (5.76)
График 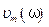 для трех значений коэффициента сопротивления (
для трех значений коэффициента сопротивления (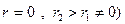 ) среды приведены на рис. 5. 18, б. Эти графики аналогичны графикам резонансных кривых
) среды приведены на рис. 5. 18, б. Эти графики аналогичны графикам резонансных кривых 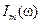 .
.
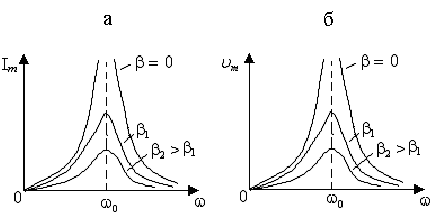
Рис. 5.18

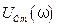 (5.67) для различных значений угловой частоты внешнего напряжения
(5.67) для различных значений угловой частоты внешнего напряжения  .
.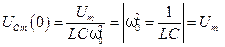 ,
, , равной нулю (
, равной нулю (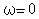 ), выходят из одной точки.
), выходят из одной точки.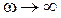 :
: 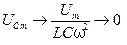 ,
, . Найдем угловую частоту
. Найдем угловую частоту 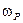 , при которой зависимость
, при которой зависимость  имеет максимальное значение. Оно будет наблюдаться в том случае, когда выражение под знаком квадратного корня в формуле (5.67) будет минимальным. Поэтому
имеет максимальное значение. Оно будет наблюдаться в том случае, когда выражение под знаком квадратного корня в формуле (5.67) будет минимальным. Поэтому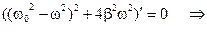
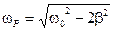 . (5.69)
. (5.69)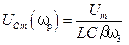 . (5.70)
. (5.70)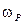 получила название резонансной частоты. В условиях малого затухания (Q > > 1) для частоты
получила название резонансной частоты. В условиях малого затухания (Q > > 1) для частоты  можно записать
можно записать , (5.71)
, (5.71)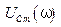 для идеального колебательного контура (
для идеального колебательного контура (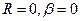 ) и для двух значений сопротивления R в нем (
) и для двух значений сопротивления R в нем (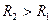 , т.е.
, т.е. 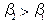 ). При этом считается, что индуктивность L катушки и электроемкость C конденсатора контура не изменяются, т.е. частота
). При этом считается, что индуктивность L катушки и электроемкость C конденсатора контура не изменяются, т.е. частота 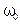 при этом остается неизменной.
при этом остается неизменной.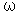 , равную
, равную 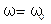 ), причем максимальное значение при этом стремится к бесконечности (рис.5.17, а). При увеличении сопротивления
), причем максимальное значение при этом стремится к бесконечности (рис.5.17, а). При увеличении сопротивления  контура коэффициент затухания
контура коэффициент затухания 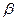 увеличивается, а максимальное значение
увеличивается, а максимальное значение 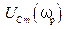 и частота
и частота 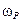 , на которую он приходится, уменьшаются (рис. 5.17, а).
, на которую он приходится, уменьшаются (рис. 5.17, а).
 для амплитуды смещения груза (м.т.) от положения равновесия можно получить, используя табл. аналогий 5.1:
для амплитуды смещения груза (м.т.) от положения равновесия можно получить, используя табл. аналогий 5.1: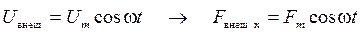 ;
;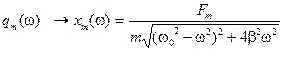 ;
; 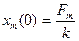 ;
; 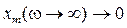 . (5.72)
. (5.72)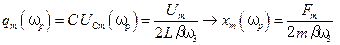 . (5.73)
. (5.73)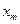 от
от 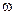 при различных значениях коэффициента затухания
при различных значениях коэффициента затухания  приведены на рис.5.17, б.
приведены на рис.5.17, б.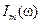 в наиболее удобном виде
в наиболее удобном виде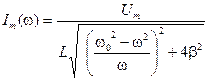 ,
, , т.е. постоянный электрический ток через цепь, содержащую конденсатор, не протекает.
, т.е. постоянный электрический ток через цепь, содержащую конденсатор, не протекает.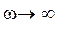 :
: 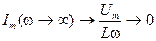 .
.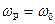 , а само максимальное значение будет равно
, а само максимальное значение будет равно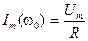 . (5.74)
. (5.74)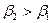 ) при постоянном значении
) при постоянном значении 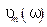 тела (м.т.) в механической системе:
тела (м.т.) в механической системе: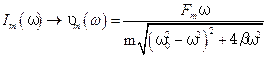 , (5.75)
, (5.75)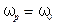 :
:  . (5.76)
. (5.76)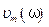 для трех значений коэффициента сопротивления (
для трех значений коэффициента сопротивления (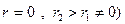 ) среды приведены на рис. 5. 18, б. Эти графики аналогичны графикам резонансных кривых
) среды приведены на рис. 5. 18, б. Эти графики аналогичны графикам резонансных кривых 



