Переменный электрический ток
Простейшей моделью генератора переменного тока является рамка площади S, содержащая N витков, которая вращается равномерно в магнитном поле с угловой частотой Рис. 5 22
Отметим, что линейная частота переменного тока в России составляет 50 Гц. Перечислим вопросы и понятия, которые вводят для описания переменного тока в электрической цепи. 1. Разность фаз колебаний между силой тока и напряжениями на конденсаторе, индуктивности и активном сопротивлении электрической цепи. Как уже было отмечено раньше (см. § 5.10.4), фаза колебаний напряжения на конденсаторе отстает по фазе от колебаний тока в цепи на π /2, а фаза колебаний напряжения на катушке опережает фазу колебаний силы тока на π /2. Фазы колебаний напряжения на активном сопротивлении R и силы тока в цепи совпадают. 2. Емкостное XC, индуктивное XL, активное R, реактивное X и полное Z сопротивления цепи. В соответствии с законом Ома для однородного участка цепи по формулам (5.67) можно ввести емкостное XC и индуктивное XL сопротивления
Они характеризуют способность катушки и конденсатора оказывать препятствие протеканию переменного электрического тока. Как видно из формул (5.84), при возрастании частоты переменного тока емкостное сопротивление XC будет уменьшаться, т.е. конденсатор оказывает меньшее препятствие протеканию тока, а индуктивное сопротивление XL будет возрастать - катушка оказывает большее препятствие протеканию переменного тока. Постоянный ток через участок цепи, содержащий конденсатор, не протекает ( Учитывая введенные сопротивления, перепишем формулу (5.68) для резонансной кривой амплитуды силы тока в контуре следующим образом:
где введены реактивное X и полное Z сопротивления цепи
3. Мощность, потребляемая электрической цепью. Учитывая разность фаз колебаний силы тока и внешнего напряжения в электрической цепи
для мгновенной мощности, потребляемой электрической цепью, получим
Ввиду малого периода колебаний переменного тока (
Согласно векторной диаграмме (см. Рис. 5.21, а, б, в)
что приводит к следующему выражению для усредненной мощности
4. Эффективные (действующие) значения силы тока и напряжения. Эти величины для гармонических колебаний вводятся по формулам
Их введение позволяет переписать формулу (5.88) без коэффициента ½, что является удобным при записи формул для средней мощности и количества теплоты в случаях переменного и постоянного тока
Отметим, что многие амперметры и вольтметры измеряют эффективные (действующие) значения силы тока и напряжения. 5. Коэффициент мощности. Входящий в формулу (5.86) коэффициент
т.е. он равен отношению активного R и полного Z сопротивлений электрической цепи. Коэффициент мощности показывает зависимость мощности, выделяемой в электрической цепи переменного тока, от разности фаз колебаний силы тока в ней и внешнего напряжения, поступающего в цепь. Так, если реактивное сопротивление цепи будет равно нулю (
|

 Переменный электрический ток также представляет собой вынужденные колебания силы тока, напряжения, происходящие в электрической цепи под действием напряжения, вырабатываемого генератором переменного тока на электростанциях. Электрическая цепь в этом случае представляет собой колебательный контур (см. рис. 5.3,
Переменный электрический ток также представляет собой вынужденные колебания силы тока, напряжения, происходящие в электрической цепи под действием напряжения, вырабатываемого генератором переменного тока на электростанциях. Электрическая цепь в этом случае представляет собой колебательный контур (см. рис. 5.3, 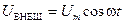 ) и поэтому здесь применимы формулы, которые были получены в § 5.10.1 – § 5.10.4.
) и поэтому здесь применимы формулы, которые были получены в § 5.10.1 – § 5.10.4.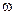 (рис. 5.22). Для максимальной ЭДС индукции
(рис. 5.22). Для максимальной ЭДС индукции  , наводимой в такой рамке, можно получить следующее выражение:
, наводимой в такой рамке, можно получить следующее выражение: ,
,  . (5.83)
. (5.83)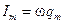 ,
,  ,
,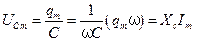 ,
, 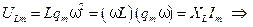
 ,
,  . (5.84)
. (5.84) =0:
=0: 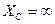 ). Индуктивное сопротивление катушки в этом случае будет равно нулю (
). Индуктивное сопротивление катушки в этом случае будет равно нулю ( ), т.е. катушка не оказывает препятствия протеканию постоянного тока. Сопротивление R, которое было введено ранее в разделе постоянный ток, называется здесь активным сопротивлением.
), т.е. катушка не оказывает препятствия протеканию постоянного тока. Сопротивление R, которое было введено ранее в разделе постоянный ток, называется здесь активным сопротивлением. ,
,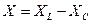 ,
,  . (5.85)
. (5.85)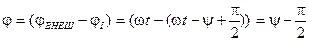 ,
,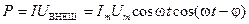 .
. ) многие приборы измеряют усредненные по времени значения мощности
) многие приборы измеряют усредненные по времени значения мощности
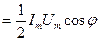 . (5.86)
. (5.86)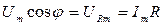 , (5.87)
, (5.87) . (5.88)
. (5.88) . (5.89)
. (5.89)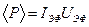 ,
,  .
.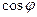 называют коэффициентом мощности. В соответствии с выражениями (5.85) и (5.87) для него можно записать
называют коэффициентом мощности. В соответствии с выражениями (5.85) и (5.87) для него можно записать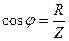 , (5.90)
, (5.90)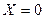 ,
, 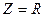 ), то тогда
), то тогда  и электрическая цепь полностью потребляет поступающую в нее энергию. При отсутствии же в цепи активного сопротивления (R =0,
и электрическая цепь полностью потребляет поступающую в нее энергию. При отсутствии же в цепи активного сопротивления (R =0, 


