Сложение взаимно перпендикулярных колебаний. Фигуры Лиссажу
Пусть тело (м.т.) одновременно участвует в двух взаимно перпендикулярных колебаниях, происходящих вдоль осей
В общем случае в результате сложения этих колебаний материальная точка будет двигаться по траектории, определяемой соотношением их частот ( Рассмотрим некоторые примеры сложения взаимно перпендикулярных колебаний. Пример 1. Делим одно уравнение (5.33) на другое и получим
т.е. траектория результирующего движения представляет собой прямую линию, лежащую в первой и третьей четвертях (рис. 5.11, а). Если разность фаз
Рис. 5.11 Получаемое при этом движение м.т. является гармоническим колебанием, так как изменение координаты r, определяющей положение м.т. на траектории движения, происходит по гармоническому закону
Такое движение м.т. также называют линейно поляризованным колебанием. Оно повторяется через время, равное периоду складываемых колебаний Пример 2.
т.е. траектория результирующего движения является эллипсом, оси которого совпадают с осями В этом случае результирующее движение м.т., движущейся по эллипсу, называют эллиптически поляризованным колебанием (для одинаковых амплитуд колебаний Рассмотрим направление движения м.т. по эллиптической траектории. В момент времени t =0 м.т. находится в точке с координатами х = А, у =0. Для разности фаз Действительно, если Если взять произвольное значение Приведенные на рис. 5.11 траектории движения м.т. называют фигурами Лиссажу. Они, в общем случае, получаются при сложении двух взаимно перпендикулярных гармонических колебаний, отношение циклических частот которых является кратным отношению целых чисел ( Если в рассмотренных примерах 1 и 2 угловые частоты складываемых колебаний незначительно отличаются друг от друга (
Это приводит к тому, что вид фигуры Лиссажу будет непрерывно изменяться, принимая вид траекторий движения, изображенных на Рис. 5.11. Поэтому, наблюдаемое во времени изменение фигуры Лиссажу означает, что частоты складываемых колебаний неодинаковы. Пример 3.
что дает фигуру Лиссажу в виде параболы (рис. 5.12, б). При других значениях разности фаз получаются фигуры Лиссажу, вид которых приведен на рис. 5.12, б и рис. 5.12, в.
Рис. 5.12 Отметим, что фигуры Лиссажу можно применять для определения частоты какого-либо гармонического колебания (сигнала). Для этого нужно на входы х и у осциллографа подать два сигнала – два гармонических колебания с известной (колебание поступает от генератора электромагнитных колебаний, его можно плавно изменять) и неизвестной частотой. Изменяя частоту генератора можно добиться устойчивой фигуры Лиссажу и, зная по ее виду отношение частот складываемых колебаний (отношение частот равно отношению числа пересечений фигуры Лиссажу прямыми, параллельными осям координат, рис. 5.13, а), определить неизвестную частоту.
|

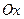 и
и 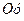 :
: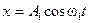 ,
,  . (5.33)
. (5.33) ), амплитуд (
), амплитуд ( ) и разности начальных фаз
) и разности начальных фаз 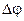 . Эти траектории можно описать уравнениями, которые не содержат явно время t и определяют зависимость координаты у от х. Форма этих траекторий и уравнения, описывающие их, и представляют интерес при таком сложении колебаний.
. Эти траектории можно описать уравнениями, которые не содержат явно время t и определяют зависимость координаты у от х. Форма этих траекторий и уравнения, описывающие их, и представляют интерес при таком сложении колебаний. .
. 
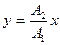 ,
, :
:  ,
, 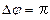 :
:  ).
).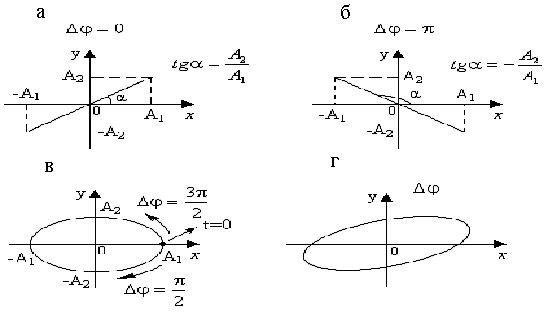
 .
. .
. :
: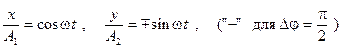 ,
, ,
,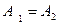 траектория движения становится окружностью, и движение м.т. называют колебаниями, поляризованными по кругу). Такие движения повторяются через время, равное периоду складываемых гармонических колебаний (
траектория движения становится окружностью, и движение м.т. называют колебаниями, поляризованными по кругу). Такие движения повторяются через время, равное периоду складываемых гармонических колебаний ( ее движение по эллиптической траектории будет происходить по направлению движения часовой стрелки, и соответственно против движения часовой стрелки для разности фаз, равной
ее движение по эллиптической траектории будет происходить по направлению движения часовой стрелки, и соответственно против движения часовой стрелки для разности фаз, равной  .
.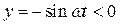 ), что соответствует движению по направлению часовой стрелки.
), что соответствует движению по направлению часовой стрелки. ), то тогда траектория результирующего движения будет также эллипсом, но ориентация его осей будет зависеть от амплитуды складываемых колебаний и разности фаз
), то тогда траектория результирующего движения будет также эллипсом, но ориентация его осей будет зависеть от амплитуды складываемых колебаний и разности фаз  ,
,  ,
,  ;
;  – целые числа). Тогда за промежуток времени, равный наименьшему кратному периодов двух складываемых колебаний
– целые числа). Тогда за промежуток времени, равный наименьшему кратному периодов двух складываемых колебаний  и
и  , движущаяся материальная точка возвращается в начальное положение - получается замкнутая линия, она называется фигурой Лиссажу.
, движущаяся материальная точка возвращается в начальное положение - получается замкнутая линия, она называется фигурой Лиссажу. ), то такое различие в частотах можно трактовать как медленное изменение во времени разности фаз складываемых колебаний
), то такое различие в частотах можно трактовать как медленное изменение во времени разности фаз складываемых колебаний .
.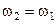 ,
,  :
: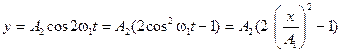 ,
,



