Введение. Сибирский государственный индустриальный университет
Учебное пособие
Редактор Комиссарова Т.И.
Подписано в печать Формат бумаги 60х84 1/16. Бумага писчая. Печать офсетная. Усл. печ. л.. Уч.изд. л.. Тираж 300 экз. Заказ Сибирский государственный индустриальный университет 654007, г. Новокузнецк, ул. Кирова, 42. Издательский центр СибГИУ ТЕОРИЯ КОЛЕБАНИЙ
Введение
Различные виды движений и процессов, происходящих в природе, можно классифицировать по-разному. По одной из таких классификаций принято выделять колебательные движения (колебания), частный случай колебательных движений – периодические колебания, и самый простой вид периодических колебаний – это гармонические колебания. К колебательным движениям (колебаниям) относят такие движения, которые характеризуются той или иной степенью повторяемости во времени описывающих их величин. К колебательным процессам можно, например, отнести механические колебания груза пружинного и математического маятников, автоколебания голосовых связок при разговоре, электромагнитные колебания силы тока, заряда, напряжения, вектора магнитной индукции
Рис.5.1
К периодическим колебаниям относятколебания, при которых описывающие их величины повторяются через промежуток времени, называемый периодом Т (рис. 5.1, б). При гармонических колебаниях (ГК) эти величины изменяются по гармоническому закону, т.е. по закону синуса или косинуса (рис. 5.1, в). ГК, как наиболее простые колебания, играют особую роль среди других видов колебаний. Оказывается, что при достаточно общих условиях, которые обычно выполняются в физических задачах, любой сложный процесс, описываемый какой-либо периодической или непериодической функцией времени f (t), можно представить в виде совокупности конечного или бесконечного набора гармонических колебаний разной частоты, т.е. представить его в виде ряда или интеграла Фурье (см. § 5.8). Это позволяет, например, предложить общую методику анализа различных временных процессов по их частотному спектру, методику воздействия сигналов на любые системы по изменению их частотного спектра и т.д. Между различными видами колебаний, такими как механические, электромагнитные, химические и т.д., происходящих в замкнутых и открытых системах, существуют много общего. Поэтому, в этом разделе наряду с рассмотрением отдельных видов колебаний изучается и то, что их объединяет, а именно: общие для них понятия (период Т, амплитуда А, фаза колебаний φ и т.д.), дифференциальные уравнения и их решения. В связи с этим широкое применение в этом разделе находит метод аналогий, при котором результаты, полученные при рассмотрении одного вида колебаний, используются для описания и других видов колебаний.
5.2. Условия возникновения колебаний в системе.
Рассмотрим подробнее аналогию между наиболее часто встречающимися в природе механическими и электромагнитными колебаниями. Для этого обсудим подробно электромагнитные колебания, происходящие в идеальном колебательном контуре (отсутствуют потери энергии колебаний на нагревание проводников), и механические колебания груза (материальной точки) пружинного маятника в отсутствии сил трения и сопротивления. Пусть в начальный момент времени (t=0, состояние 1) груз пружинного маятника максимально отклонен от положения равновесия (х=хm, рис. 5.2, а), а на обкладки конденсатора колебательного контура сообщают максимальный заряд (q=qm, рис. 5.2, б). Состояние 1 пружинного маятника характеризуется тем, что скорость груза и его кинетическая энергия равны нулю, а полная энергия колебаний равна максимальной потенциальной энергии пружины. Для колебательного контура в состоянии 1 сила тока и энергия магнитного поля катушки равны нулю, а полная энергия колебаний совпадает с максимальной энергией электрического поля конденсатора. t=0, Состояние 1. Пружинный маятник:
колебательный контур:
В течение времени 0< t< T/4 происходят следующие процессы. Пружинный маятник. Под действием силы упругости груз начинает двигаться, скорость груза нарастает постепенно из-за наличия у него инерционных свойств (массы) и в момент времени t, равный четверти периода колебаний Т (t=T/4) груз проходит положение равновесия (состояние 2, рис. 5.2, а). При этом потенциальная энергия пружины полностью переходит в кинетическую энергию груза. Колебательный контур. Конденсатор начинает разряжаться, сила тока в кон-
Рис. 5.2 туре возрастает постепенно из-за возникновения в катушке э.д.с. самоиндукции, которая препятствует нарастанию основного тока в контуре. Сила тока достигает максимального значения в момент времени t=T/4 (состояние 2, рис. 5.2, б). При этом энергия электрического поля конденсатора полностью переходит в энергию магнитного поля катушки. t=Т/4, Состояние 2. Пружинный маятник:
колебательный контур:
В следующие четверть периода (T/4< t< T/2) наблюдаются такие процессы. Пружинный маятник. Под действием силы упругости скорость груза начинает уменьшаться, она уменьшается постепенно из-за наличия у груза массы и в момент времени t= T/2 (состояние 3, рис. 5.2, а) она обращается в ноль, кинетическая энергия груза полностью переходит в потенциальную энергию сжатой пружины. Колебательный контур. Сила тока в контуре начинает убывать, убывает она постепенно, так как в катушке возникает ток самоиндукции, который препятствует убыванию основного тока в контуре, и в момент времени t= T/2 (состояние 3, рис. 5.2, б) сила тока обращается в ноль. Конденсатор перезаряжается, энергия магнитного поля катушки полностью переходит в энергию электрического поля конденсатора. t=Т/2, Состояние 3. Пружинный маятник:
колебательный контур:
Из описанных выше колебательных процессов можно сделать вывод об условиях возникновения колебаний в любой системе, а именно: система должна обладать 1) устойчивым положением равновесия; 2) инерционными свойствами; 3) малыми потерями энергии колебаний (на преодоление сил трения в случае механических колебаний и на нагревание проводников в случае электромагнитных колебаний в контуре). Рассмотренные примеры позволяют установить аналогию между механическими и электромагнитными колебаниями, которая отражена в табл.5.1 Таблица 5.1
С помощью данной таблицы можно записывать формулы для одного вида колебаний, если известны аналогичные формулы для другого вида колебаний. Так, например,
В дальнейшем эта таблица будет использоваться для записи без вывода различных формул теории колебаний.
|
магнитного поля катушки в колебательном контуре, периодические колебания цвета продуктов некоторых химических реакций и т.д. На Рис. 5.1, а в качестве примера колебательного движения приведена зависимость от времени t смещения х груза (материальной точки) пружинного маятника от положения равновесия.
.
.
;
.
;
.
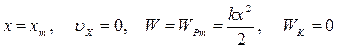(С - электроемкость конденсатора)
, 
,
, 
.
