Стоячие волны. Колебания струны
Стоячей волной называют волну, образующуюся при сложении двух встречных волн одинаковой частоты и амплитуды
Для простоты здесь рассмотрен случай сложения двух плоских волн, распространяющихся вдоль оси Ох в положительном (
Из формулы (6.21) следует, что амплитуда стоячей волны
зависит от координаты Найдем координаты точек пространства (
Из формул (6.23) и (6.24) следует, что расстояние между соседними узлами На рис. 6.7 приведены фотографии стоячей волны для трех моментов времени t=0, Т/4, Т/2. На них стрелками указаны направления движения частиц среды. Из графиков видно, что все частицы среды, находящиеся между соседними узлами, совершают колебания с разными амплитудами и с одинаковой фазой (частицы одновременно достигают положения равновесия и движутся в одну сторону). При переходе через узел фаза колебаний частиц изменяется на Как следует из графиков, приведенных на рис. 6.7, при образовании в среде стоячей волны в среде не происходит переноса энергии от источника
Рис. 6.7
колебаний, так как положение узлов и пучностей с течением времени не изменяется; перенос энергии встречных волн одинаковый и происходит в противоположных направлениях. Наблюдается переход потенциальной энергии колебаний, сосредоточенной в основном в узлах см. (рис. 6.7, момент времени Действительно в соответствии с формулами (6.10), (6.12) и (6.21) для кинетической и потенциальной энергий частиц в случае стоячей волны можно записать следующие формулы
из которых видно, что наибольшая потенциальная энергия частиц наблюдается в узлах стоячей волны ( Стоячие волны обычно образуются при отражении бегущей волны от границы раздела двух сред. При этом возможны два случая. В первом случае при отражении волны от более плотной среды фаза волны изменяется на значение, равное
Если, например, в деревянной линейке, закрепленной на одном конце, возбудить стоячую волну, то на втором свободном конце будет либо пучность (отражение бегущей по линейке волны от границы раздела дерево – воздух, рис. 6.8, а), либо узел стоячей волны (отражение бегущей по линейке волны от границы раздела «дерево-вода», рис. 6.8, б). Причем на длине линейки укладывается половина длины волны. Наиболее наглядным примером стоячей волны являются колебания струны, закрепленной на концах. Возбуждение в ней поперечных колебаний приводит к образованию стоячей волны, узлы которой приходятся на закрепленные концы
Рис. 6.8 (см. § 5.13, рис. 5.27, в и рис. 6.8, в). На длине струны
Любое произвольное колебание струны можно представить в виде суммы ее нормальных колебаний.
|

 ,
,  .
. ) и отрицательном (
) и отрицательном ( ) ее направлениях. Для уравнения стоячей волны в соответствии с формулой сложения косинусов можно записать
) ее направлениях. Для уравнения стоячей волны в соответствии с формулой сложения косинусов можно записать . (6.21)
. (6.21) (6.22)
(6.22)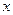 выбранной точки пространства, изменяясь от минимального значения, равного нулю, до максимального значения, равного 2 А.
выбранной точки пространства, изменяясь от минимального значения, равного нулю, до максимального значения, равного 2 А. ), в которых наблюдается максимальная амплитуда колебаний частиц среды, их называют пучностями стоячей волны, и координаты узлов стоячей волны (
), в которых наблюдается максимальная амплитуда колебаний частиц среды, их называют пучностями стоячей волны, и координаты узлов стоячей волны ( ), для них амплитуда колебаний частиц среды равна нулю
), для них амплитуда колебаний частиц среды равна нулю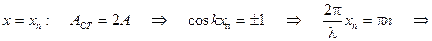
 (6.23)
(6.23)
 (6.24)
(6.24) и соседними пучностями
и соседними пучностями  стоячей волны одинаково и равно
стоячей волны одинаково и равно  .
. (частицы по разные стороны от узла одновременно достигают положения равновесия и движутся в противоположных направлениях).
(частицы по разные стороны от узла одновременно достигают положения равновесия и движутся в противоположных направлениях).
 ), в кинетическую энергию колебаний, сосредоточенную в основном в пучностях стоячей волны см. (рис. 6.7, момент времени
), в кинетическую энергию колебаний, сосредоточенную в основном в пучностях стоячей волны см. (рис. 6.7, момент времени 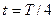 ) и наоборот. Средний же по времени поток энергии в любом сечении стоячей волны равен нулю.
) и наоборот. Средний же по времени поток энергии в любом сечении стоячей волны равен нулю. ,
, ,
, ), а наибольшая кинетическая энергия частиц будет в пучностях стоячей волны (
), а наибольшая кинетическая энергия частиц будет в пучностях стоячей волны ( ).
). ) образуется узел стоячей волны
) образуется узел стоячей волны  Во втором случае при отражении волны от менее плотной среды фаза волны не изменяется, и на границе раздела (
Во втором случае при отражении волны от менее плотной среды фаза волны не изменяется, и на границе раздела (
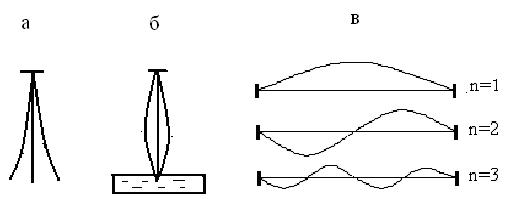
 укладывается целое число полуволн, что позволяет найти частоты нормальных колебаний струны (§ 5.13, формула (5.92)):
укладывается целое число полуволн, что позволяет найти частоты нормальных колебаний струны (§ 5.13, формула (5.92)): ,
, 
 , n= 1, 2, 3, …
, n= 1, 2, 3, …


