Волновой пакет. Групповая скорость. Дисперсия волн
Гармоническая (синусоидальная) волна с частотой В реальных случаях время излучения Вводят понятие волнового пакета – это группа волн, занимающая в каждый данный момент времени ограниченную область пространства (рис. 6.10).
Рис. 6.10
Для описания движения волнового пакета вводят понятие групповой скорости Для того чтобы записать формулу для групповой скорости волнового пакета, поступим следующим образом: 1. Возьмем линейную среду, для которой выполняется принцип суперпозиции, а именно, возмущение, возникающее в среде при распространении группы волн, можно представить как сумму возмущений, которые возникают в среде при распространении в среде только одной волны этой группы. Этот принцип суперпозиции позволяет представить волновой пакет в виде суммы гармонических волн, частота которых заключена в узком интервале частот ( 2. Рассмотрим частный случай волнового пакета, состоящего из двух гармонических волн одинаковой амплитуды с близкими значениями циклических частот (
причем
Складывая эти волны, можно получить
Первый сомножитель в этом выражении изменяется значительно медленнее со временем
Максимальное значение амплитуды волнового пакета (оно соответствует точке В на рис. 6.10) наблюдается при фазе колебаний, равной нулю, что приводит к следующей формуле для групповой скорости
где учтено, что интервалы Полученная формула для групповой скорости (6.29) будет справедливой и в общем случае. 3. Введем понятие дисперсии волн. Под явлением дисперсии волн понимают зависимость фазовой скорости волны от частоты или длины волны ( Для линейной среды в отсутствии явления дисперсии ( 4. Рассмотрим диспергирующие среды – это среды, в которых наблюдаются явления дисперсии. Для этих сред между групповой скоростью волнового пакета и фазовой скоростью составляющих его волн можно получить следующую формулу связи
Из выражения (6.30) видно, что при наличии явления дисперсии ( Явление нормальной дисперсии наблюдается для прозрачных сред, а аномальной дисперсии – для сред, поглощающих излучение. Причем, для сред с большим коэффициентом поглощения групповая скорость не вводится Это связано с тем, что в таких средах волновой пакет резко изменяет свою форму, а потеря энергии, приводит к тому, что понятие групповой скорости, как скорости переноса энергии утрачивает свой смысл. Понятие групповой скорости используется в методах измерения скоростей распространения волн. Именно она фигурирует при измерении дальности в гидро- и радиолокации, в методах зондирования ионосферы, в системах управления космическими объектами и т.д. Отметим, что, согласно теории относительности, групповая скорость всегда меньше скорости света в вакууме (
|

 является идеализацией, т.е. в реальных случаях ее не существует. Это связано с тем, что для нее разброс по частотам
является идеализацией, т.е. в реальных случаях ее не существует. Это связано с тем, что для нее разброс по частотам  равен нулю (
равен нулю ( ). Поэтому, в соответствии с формулой (5.43), время излучения такой волны стремится к бесконечности (
). Поэтому, в соответствии с формулой (5.43), время излучения такой волны стремится к бесконечности (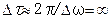 ). Это означает, что такая синусоидальная волна занимает все пространство (
). Это означает, что такая синусоидальная волна занимает все пространство (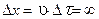 ) и никакой полезной информации в себе не несет.
) и никакой полезной информации в себе не несет.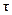 волны частоты
волны частоты 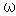 является конечным, т.е. волна занимает ограниченную область пространства (
является конечным, т.е. волна занимает ограниченную область пространства ( ) и имеет не равный нулю разброс по частотам (
) и имеет не равный нулю разброс по частотам (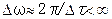 ), т.е. представляет собой группу волн.
), т.е. представляет собой группу волн.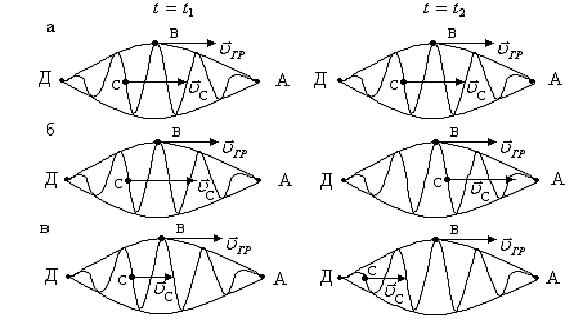
 как: 1) скорости движения центра волнового пакета; 2) скорости движения максимального значения его амплитуды (например, точки В на рис. 6.10); 3) скорости переноса энергии волнового пакета.
как: 1) скорости движения центра волнового пакета; 2) скорости движения максимального значения его амплитуды (например, точки В на рис. 6.10); 3) скорости переноса энергии волнового пакета.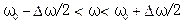 ,
, 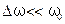 ), и модулей волновых чисел в интервале (
), и модулей волновых чисел в интервале (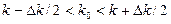 ,
, 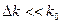 ), где под
), где под 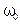 можно понимать частоту этого волнового пакета.
можно понимать частоту этого волнового пакета.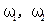 ) и волновых чисел (
) и волновых чисел (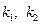 ):
):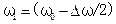 ,
,  и
и 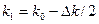 ,
,  ,
,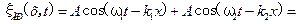
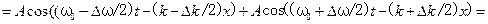
 .
. и координатой
и координатой  , чем второй, и представляет собой амплитуду
, чем второй, и представляет собой амплитуду 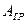 волнового пакета
волнового пакета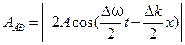 .
.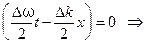
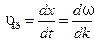 , (6.29)
, (6.29) частот и модулей
частот и модулей 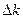 волновых векторов являются малыми и поэтому их можно записать в виде
волновых векторов являются малыми и поэтому их можно записать в виде 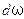 и
и 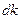 .
. ).
).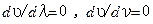 ), все фазовые скорости волн, составляющих волновой пакет, будут одинаковы и равны групповой скорости волнового пакета. Например, на рис. 6.10, а в разные моменты времени положение точки С относительно центра волнового пакета и относительно других составляющих этот пакет волн не изменяется:
), все фазовые скорости волн, составляющих волновой пакет, будут одинаковы и равны групповой скорости волнового пакета. Например, на рис. 6.10, а в разные моменты времени положение точки С относительно центра волнового пакета и относительно других составляющих этот пакет волн не изменяется:  .
. ,
,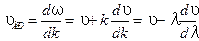 . (6.30)
. (6.30)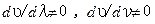 ) фазовые скорости
) фазовые скорости 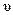 волн будут отличаться от групповой скорости волнового пакета. При этом различают два случая: 1) нормальная дисперсия (
волн будут отличаться от групповой скорости волнового пакета. При этом различают два случая: 1) нормальная дисперсия ( 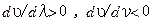 ) наблюдается для тех сред, для которых фазовая скорость волн будет превышать групповую скорость:
) наблюдается для тех сред, для которых фазовая скорость волн будет превышать групповую скорость: 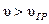 . Так, например, на рис. 6.10, б фиксированное значение фазы волны для точки С перемещается внутри волнового пакета к его конечной точке А, т.е.
. Так, например, на рис. 6.10, б фиксированное значение фазы волны для точки С перемещается внутри волнового пакета к его конечной точке А, т.е. 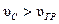 );
); 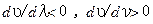 ) наблюдается в тех случаях, когда фазовая скорость волн, составляющих волновой пакет, будет меньше групповой скорости:
) наблюдается в тех случаях, когда фазовая скорость волн, составляющих волновой пакет, будет меньше групповой скорости: 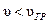 (фиксированное значение фазы волны для точки С перемещается внутри волнового пакета к начальной точке D).
(фиксированное значение фазы волны для точки С перемещается внутри волнового пакета к начальной точке D).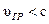 ).
).


