Электромагнитные волны
6.2.1. Волновые уравнения для электромагнитной волны (ЭМВ). В § 4.2.8 было отмечено, что из полной системы уравнений Максвелла вытекает существование электромагнитного поля в виде ЭМВ. Покажем это на конкретном примере. Пусть имеется однородная, изотропная пластина из диэлектрика (рис. 6.13, а), заполняющая полупространство ( Запишем первое уравнение Максвелла в дифференциальной форме (формула (4.67)):
Из начальных условий и соображений симметрии для рассматриваемого примера следует, что зависимости вектора
Оставим только зависящие от времени решения, так как только они приводят к возникновению ЭМВ в среде, и в итоге получим одно скалярное уравнение
Аналогично, из второго уравнения Максвелла можно записать
Возьмем частную производную по координате х от уравнения (6.41) и частную производную по времени t от уравнения (6.42):
Аналогично, беря частные производные по времени t от (6.41) и по координате х от (6.42), получим
Если сопоставить выражения (6.43) и (6.44) с уравнением (6.6), то можно сказать, что они являются волновыми уравнениями. Решением этих волновых уравнений являются плоские монохроматические волны электрического и магнитного полей
распространяющихся вдоль оси Ох с фазовой скоростью
где с - скорость света в вакууме. Итак, ЭМВ представляет собой распространяющиеся в пространстве две волны электрического и магнитного полей, взаимосвязанных друг с другом, порождающих одна другую. В общем случае волновые уравнения для ЭМВ будут соответствовать волновому уравнению (6.7):
|

 , рис. 6.13, а). Во всех точках плоскости уОz, на входе пластинысоздаются гармонические колебания вектора напряженности электрического поля вдоль оси Оу
, рис. 6.13, а). Во всех точках плоскости уОz, на входе пластинысоздаются гармонические колебания вектора напряженности электрического поля вдоль оси Оу  .Считается, что в пластине отсутствуют электрические заряды (q =0) и токи проводимости (j пр=0), а значения относительных диэлектрической и магнитной проницаемостей среды являются постоянными, т.е. среда не является ферромагнитной и сегнетоэлектрической.
.Считается, что в пластине отсутствуют электрические заряды (q =0) и токи проводимости (j пр=0), а значения относительных диэлектрической и магнитной проницаемостей среды являются постоянными, т.е. среда не является ферромагнитной и сегнетоэлектрической.
 .
. от координат у и z не будет, также не будет составляющей вектора
от координат у и z не будет, также не будет составляющей вектора 

 ,
,  ,
, 
 .
. ,
, . (6.42)
. (6.42)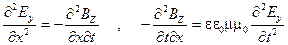 ,
, . (6.43)
. (6.43) ,
,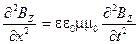 . (6.44)
. (6.44) , (6.45)
, (6.45) , (6.46)
, (6.46) , (6.47)
, (6.47) ,
,  . (6.48)
. (6.48)


